'e2> = <Blanks e1''e2>
3. ОСНОВНЫЕ ПРИЕМЫ ПРОГРАММИРОВАНИЯ
Средства языка, которые были введены до сих пор, составляют уровень, который известен как базисный РЕФАЛ. Расширение этого языка, которое предоставит некоторые дополнительные средства программирования, будет описано в следующей главе. Начнем с основных приемов программирования на базисном РЕФАЛе.
3.1. КРУГЛЫЕ СКОБКИ КАК УКАЗАТЕЛИ
Чтобы проиллюстрировать процесс создания программы на РЕФАЛе, предположим, что мы хотим написать программу, которая удаляет все лишние пробелы в данной строке символов, т.е. замещает каждую группу подряд стоящих пробелов единственным пробелом. Назовем функцию, выполняющую эту работу, Blanks. Мы приходим к самому очевидному решению, рассуждая следующим образом: нам не нужны соседние пробелы; поэтому, как только обнаруживается пара соседних пробелов, следует удалить один из них и повторять это до тех пор, пока имеются такие пары. В результате получаем предложение:
<Blanks e1'
(для удобочитаемости пробелы замещены знаками '
').
ЗАМЕЧАНИЕ: При рассмотрении отдельного
РЕФАЛ-предложения удобно записывать его левую
часть полностью, т.е. как вызов функции, который
состоит из имени функции и угловых скобок
вызова функции.
Если это предложение оказывается неприменимым, желаемый результат достигнут, и работа завершается при помощи предложения:
<Blanks e1> = e1
Таким образом, определение функции имеет вид:
Blanks {
e1'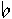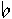'e2 = <Blanks e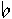1''e2>;
e1 = e1; }
Проанализируем алгоритмическую эффективность нашей программы. Какие действия будет выполнять РЕФАЛ-интерпретатор, вычисляя эту функцию?
Переменная e1 в первом предложении
является открытой. Первоначально она
принимает пустое значение, а затем удлиняется до
тех пор, пока не будет найдена первая комбинация '
' (если таковая имеется) .
Переменная e2 является закрытой;
поэтому оставшаяся часть аргумента не
просматривается. Так как мы очевидно должны
просматривать аргумент при поиске первых
соседних пробелов, ни одного лишнего действия
пока еще не совершено.
Теперь наступает очередь замещения. Умный интерпретатор определит, сравнивая левую и правую части предложения, что для выполнения замещения нужно только исключить один из пробелов. Более ограниченный интерпретатор построит замещение из фрагментов поля зрения, на которые была спроектирована левая часть. В зависимости от степени интеллекта, интерпретатор может использовать те же пробел и скобки вызова функции, которые стоят в левой части, или отбрасывать их и вставлять новые; но он, конечно, не будет просматривать или копировать значения переменных e1 и e2, так как это привело бы к нарушению требования 2 к эффективности интерпретации. За счет манипулирования адресами в компьютерной памяти значения e1 и e2 будут просто перемещены из одного места в другое. Эта операция потребует постоянного времени, которое не зависит от размера обрабатываемых выражений. При анализе алгоритмов обычно желательно знать, как время выполнения алгоритма зависит от размера обрабатываемых им объектов. Такая зависимость имеет решающее значение, в то время как постоянные кванты времени выполнения составляющих операторов, которые зависят от конкретной реализации алгоритма или от скорости компьютера, имеют второстепенное значение. Следовательно, в нашем случае работа РЕФАЛ-интерпретатора является безусловно эффективной.
На следующем шаге работы РЕФАЛ-машины весь аргумент Blanks , включая проекцию e1 , будет просмотрен снова при поиске пары смежных пробелов. И это является очевидной потерей времени, так как проекция e1 не может содержать такую пару. Это является недостатком нашей программы, и можно скорректировать ее, вынося e1 за пределы вычислительных скобок в правой части. Один пробел, разумеется, должен остаться слева внутри скобок. Определение приобретает вид:
Blanks {
e1'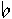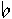'e2 = e1 <Blanks '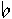'e2>;
e1 = e1; }
Теперь алгоритм, скрывающийся за нашим определением, полностью эффективен.
Когда вычисляется функция Blanks , левая скобка вызова функции используется как указатель, который отделяет обработанную часть строки от части, еще не подвергавшейся обработке. Рассмотрим пример, где скобки вызова функции не могут использоваться подобным образом. Допустим, желательно определить корректирующую функцию Correct , уничтожающую в заданной строке символов всякий символ, за которым следует знак уничтожения '#' . Если в строке имеется несколько знаков уничтожения, функция ликвидирует соответствующее число предшествующих им символов. Так, если набрана строка 'Crocodyle', а затем замечена ошибка, можно продолжить:
Crocodyle###iles were everywe#here
и если Correct применяется к этой строке, результатом будет:
Crocodiles were everywhere
Прямое определение, которое хочется записать, не заботясь об эффективности, имеет вид:
Correct {
e1 sA'#' e2 = <Correct e1 e2>;
e1 = e1; }
Согласно этому алгоритму аргумент будет просматриваться с начала столько раз, сколько в нем встречается символов уничтожения. Для улучшения этой ситуации нельзя просто вынести строку e1 за пределы скобок вызова функции, так как ее правый конец может еще нуждаться в коррекции. Что можно было бы сделать, если бы программирование велось на машинном языке? После первого шага можно было бы поместить указатель в ту позицию строки, где производится действие, т.е. где надлежит уничтожить символ:
Crocodyl^##iles were everywe#here
Указатель, который представлен символом ^ , является адресом в компьютере, который позволяет добраться до нужной позиции за один прыжок. Тогда на следующем шаге можно было бы не просматривать Crocodyl , но, просто совершив прыжок по указателю, увидеть, что следующим символом снова является знак уничтожения, и уничтожить предшествующий символ 'l' . На каждом следующем шаге можно было бы начинать просмотр снова с прыжка по указателю.
То же самое можно сделать и на РЕФАЛе. Структурные скобки будут служить указателями. В самом деле, согласно требованию эффективности 1, с каждой круглой скобкой должен быть связан адрес сопряженной ей скобки, так что возможен мгновенный переход от одной скобки к другой. По отношению к функции Correct это означает, что следует заключать в скобки начало строки, которое уже просмотрено. Первоначальным аргументом должно быть:
() Crocodyle###iles were everywe#here
После первого использования знака уничтожения аргумент приобретет вид:
(Crocodyl) ##iles were everywe#here
и т.д.. Правая скобка здесь по существу является указателем.
Если желательно сохранить формат функции Correct таким, каким он был определен ранее, т.е. просто <Correct_e.String> , то следует ввести вспомогательную функцию, скажем Cor , в формате:
<Cor (e.Scanned-already) e.Not-yet-scanned>
Эффективно будет работать следующее определение:
Correct {
e1 = <Cor () e1>; }
Cor {
*1.A delete sign after the pointer;
* step back and delete
(e1 sX) '#'e2 = <Cor (e1) e2>;
*2.Look forward for the next delete sign;
* delete and move pointer
(e1) e2 sX '#'e3 = <Cor (e1 e2) e3>;
*3.No signes to delete
(e1) e2 = e2; }
Упражнение 3.1 Проанализировать, что происходит при вычислении
<Correct 'c##Crocodile'>
Переопределить Cor таким образом, чтобы выдавалось предупреждение 'Extra delete signs!' в подобных ситуациях.
С формальной точки зрения все РЕФАЛ-функции являются функциями одного аргумента. Однако очень часто этот единственный аргумент состоит из частей, которые по существу являются подаргументами (но обычно называются просто аргументами). Когда определяется функция, на самом деле представляющая собой функцию нескольких аргументов, производится объединение этих аргументов каким-либо образом, чтобы образовать единственный формальный аргумент. Это задает формат функций.
Программируя на РЕФАЛе, можно выбирать любые форматы. В принципе можно разделять подаргументы некоторыми символами, например, запятыми:
<F e1','e2> <G e1','e2','e3>
Одним из недостатков этого метода является то, что, как известно, аргументы не должны включать разделители -- в данном случае запятые. Но существует еще более серьезное возражение против таких форматов: они включают открытые e-переменные, которые подразумевают, что значения аргументов будут просматриваться даже тогда, когда это не требуется по сути алгоритма. Вот почему в форматах следует использовать круглые скобки.
Чтобы разделить два подвыражения, требуется только одна пара круглых скобок; для трех подвыражений потребуется две пары, и т.д. Но ничто не мешает заключать каждый подаргумент в круглые скобки. Таким образом, имеется очевидная свобода в выборе форматов:
<F (e1)e2> <F e1(e2)> <F (e1)(e2)> <F (e1)(e2)e3> <F (e1)e2(e3)>
и т.д. Можно варьировать форматы, включая мнемонические символы или строки, например:
<F Graph (e.Gr) Start (e.St) Weights (eW)>
Настоятельно рекомендуется, чтобы форматы функций, когда они являются нетривиальными, снабжались в программе комментариями. Также желательно указывать форму и тип значения функции. Хотя такие комментарии не являются необходимыми (и обычно опускаются для простых функций), они значительно повышают читабельность программы и неоценимы при отладке. Конкретная форма комментариев оставляется на усмотрение пользователя. В этой книге используется следующая форма:
* < Function-name Argument > * == Result-1 * == Result-2 ... etc.
В то время как единственный знак равенства в РЕФАЛе символизирует один шаг РЕФАЛ-машины, сдвоенный знак равенства говорит о том, что должно произойти после некоторого точно не установленного количества шагов машины, т.е. когда процесс вычислений завершен. Часто результат может иметь одну из возможных форм. Если форма результата более или менее очевидна, эта часть опускается.
Комментарии к определению функции Cor из Разд. 3.1 могли бы иметь такой вид:
* <Cor (e.Scanned-already) e.Not-yet-scanned> * == e.Corrected
Имя переменной, как всегда в программировании, может давать представление о том, чем она является. В РЕФАЛе имена переменных, используемые в различных предложениях, совершенно независимы; и, разумеется, имена переменных в комментариях не играют никакой роли. Но полезной является практика выбора имен переменных таким образом, чтобы они были идентичными или, по крайней мере, похожими в различных предложениях и так, чтобы они походили на имена переменных в форматах, даже если это односимвольное имя. Сопоставление предложения с форматом помогает читать программу.
В следующем упражнении приводится пример
функции с более сложным форматом.
Упражнение 3.2 Определить функцию <Cut_e1__e2_>
, которая рассекает выражения e1 и e2
на части так, что они оканчиваются одинаковыми
термами, имеющими одинаковые порядковые номера в
соответствующих выражениях. Эти части должны
быть заключены в круглые скобки и выданы на
печать попарно. Оставшиеся части выражений,
которые не сопоставляются, должны быть
отброшены. Например, если два выражения имеют
вид:
'abcc++'()'y'('!')'yxrtr'
'xyzz+'('==')'yy'('!')'**x'(())'pq'
то вывод на печать должен выглядеть следующим образом:
(abcc+)(xyzz+) (+()y)((==)yy) ((!))((!))
В РЕФАЛе нет других типов данных, кроме трех синтаксических категорий: символ, терм, выражение. Вследствие этого язык становится очень простым для программирования и формального анализа, все еще позволяя легко имитировать в рамках его простого синтаксиса многое из того, что достигается введением типов данных. Предположим, например, что нужно оперировать с рациональными числами, которые представлены тремя символами: знак, числитель, знаменатель. Мы вводим имя Rat для такой структуры данных и используем ее в следующей форме:
(Rat s.Sign s.Numerator s.Denominator)
Нет необходимости связывать специальный тип с переменными этого типа данных. Для произвольного рационального числа 'X' мы просто запишем:
(Rat eX)
Произвольное отрицательное рациональное число может быть записано как:
(Rat '-'eX)
Для каждого типа данных легко можно определить функции доступа, которые предусматривают выделение структурных компонент, например:
Numerator { (Rat sS sN sD) = sN}
Однако очень часто использование функций доступа не нужно; прямое использование образцов делает определение и более кратким, и более ясным. Например, умножение рациональных чисел можно определить следующим образом:
Mul{
(Rat s.S1 s.N1 s.D1)(Rat s.S2 s.N2 s.D2) =
(Rat <Mul-signs s.S1 s.S2>
<* s.N1 s.N2> <* s.D1 s.D2>);
}
где функция Mul-signs должна быть определена соответствующим образом. (Здесь, как и выше, оставлен открытым вопрос о том, как представить рациональное число 0) .
Вернемся к функции Blanks, определенной в
Разд. 3.1. Теперь желательно модифицировать ее так,
чтобы исключались только те повторяющиеся
пробелы, которые не заключены в кавычки -- обычная
ситуация в языках программирования. В этом
случае невозможно использовать образец e1''e2 с открытой e-переменной, но
следует обозревать символы один за другим.
Прежде всего, переопределим старую функцию Blanks
следующим образом:
Blanks {
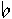
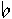''e1 = <Blanks ''e1>;
sA e1 = sA <Blanks e1>;
* End of job
= ; };
Здесь открывающая скобка вызова функции ('указатель') продвигается посимвольно, в то время как результат накапливается в поле зрения. Теперь можно модифицировать это определение, добавив два предложения на случай, когда следующим символом является кавычка:
Blanks {
*1.Delete one of two adjacent blanks
''e1 = <Blanks ''e1>;
*2.If a quote, jump to the next quote
''e1'' e2 = ''e1'' <Blanks e2>;
*3.No pair for a quote: an error
'' e1 =
<Prout 'ERROR: no pair for quote in 'e1>;
*4.Regular symbol
sA e1 = sA <Blanks e1>;
*5.End of job
= ; };
Как упомянуто в Главе 1, изолированная кавычка представляется в РЕФАЛе (как и во многих других языках программирования) двойной кавычкой, и точно так же представляется кавычка внутри строки. Заметим, что Blanks корректно работает, если встречается кавычка - как изолированная, так и внутри строки.
Где бы ни встретились в алгоритме открытые переменные, они должны применяться с целью эффективности его выполнения. Если даже алгоритм с открытой переменной может быть по существу таким же, как в случае посимвольной обработки, ряд шагов РЕФАЛ-машины может стать короче. Из-за накладных расходов реализации шага программа с открытыми переменными будет работать быстрее. В последнем определении Blanks оставлены открытые переменные, а именно e1 в предложении 2, для того, чтобы совершить прыжок прямо к закрывающей кавычке.
Следует упомянуть, однако, что когда имеется более чем одна открытая переменная, универсальный алгоритм сопоставления, описанный в Главе 2, может и не являться наиболее эффективным решением проблемы.
Рассмотрим предложение:
<Sub-a-z e1 'a'eX'z' e2> = (e1) 'a'eX'z' (e2)
Оно выделяет подстроку, которая начинается с 'a' и заканчивается 'z' . Если аргумент в самом деле содержит такую подстроку, алгоритм будет работать вполне эффективно. Первое вхождение 'a' будет обнаружено, а затем и первое вхождение 'z' за ним. Но предположим, что аргумент не содержит ни одного символа 'z', однако в нем есть множество символов 'a', например:
'abababababababababababababababababababaababab'
Тогда машина выделяет первое 'a' , терпит неудачу в поиске 'z' , удлиняет e1 , вновь терпит неудачу в поиске 'z' , вновь удлиняет e1 , и т.д.: наблюдается квадратичная зависимость количества операций от длины выражения вместо линейной.
Во избежание подобной неэффективности, следует встроить обработку в две функции, наподобие:
Sub-a-z {
e1'a'e2 = <Find-z (e1'a')e2>;
/* Find 'a' and pass the argument to Find-z */
e2 = <Prout 'No substring a-z'>; }
Find-z {
(e1'a') eX'z'e2 = (e1) 'A'e1'z' (e2);
(e1) e2 = <Prout 'No substring a-z'>;
}
Вообще говоря, всегда есть надежное средство, чтобы представить линейный просмотр как процесс сопоставления с одной открытой переменной. При наличии нескольких открытых переменных, если речь идет об эффективности, необходим специальный просмотр в каждом отдельном случае. Переопределение с целью избежать возможной неэффективности, как в приведенном выше примере, обычно является довольно легким.
Открытые и повторные e-переменные, так же как и повторные t-переменные, позволяют скрывать за образцом рекурсию. Если по какой-либо причине желательно все циклы рекурсии сделать явными (и мы действительно хотим этого в ходе функциональной трансформации), можно переписать каждое определение таким образом, чтобы оно не использовало переменные указанных типов. Например, функция Sub-a-z не выглядит рекурсивной: она либо вызывает Find-z (которая никогда не вызывает Sub-a-z ), либо встроенную функцию Prout . Но на самом деле она является рекурсивной из-за наличия открытой переменной в первом предложении. Она может быть переопределена следующим образом:
Sub-a-z {
e1 = <Sub-a-z-1 ()e1>; }
Sub-a-z-1 {
*1.'a' is found. Control is passed to Find-z.
(e1) 'a'e2 = <Find-z (e1'a') e2>;
*2.Recursion: jump over any symbol distinct
* from 'a'.
(e1) sX e2 = <Find-a-z-1 (e1 sX) e2>;
*3.The string is exhausted without finding 'a'
(e1) = <Prout 'No substring a-z'>; }
Можно было бы заметить, что используется некая
система в переписывании определений этой
функции. Она состоит в заключении открытых
переменных в скобки и во введении
вспомогательных функций, которые имитируют
удлинение открытых переменных. Этот процесс
исключения неявной рекурсии можно легко
запрограммировать и выполнять автоматически.
Упражнение 3.3 Функцию проверки равенства
произвольных выражений (не обязательно
являющихся строками) можно определить следующим
образом:
Equal {
(e1)(e1) = T;
(e1)(e2) = F; }
Переопределить ее так, чтобы исключить неявную
рекурсию.
Упражнение 3.4 Исключить неявную рекурсию в
следующем определении:
F {
e1 sX e2 sX e3 = sX e2 sX;
e1 = <Prout 'No repeated symbols'>; }
Сравнить оба определения по эффективности.
Упражнение 3.5 Конечное множество символов
может быть представлено строками, включающими те
и только те символы, которые входят в это
множество. Определить функцию <Isect
(e.Set1)e.Set2>, которая вычисляет пересечение
двух множеств. Определить ее как с
использованием открытых e-переменных, так и без
него.
Если количество вхождений свободной переменной в правую часть предложения превышает количество ее вхождений в левую часть, ее значение должно быть продублировано интерпретатором, когда он применяется к этому предложению. Это следует принимать во внимание при программировании, так как бесполезное дублирование переменных может приводить к существенным потерям в эффективности. В более сложных реализациях РЕФАЛа, чем простой интерпретатор, излишнего дублирования объектных выражений можно избежать, используя указатели для некоторых частей исходных выражений. Но, программируя для интерпретатора и мысля о РЕФАЛ-программах в терминах простого пошагового выполнения, следует принимать на себя полную ответственность за избежание бесполезного дублирования.
Эти рассмотрения имеют прямое отношение к способу, которым определяется ветвление в РЕФАЛе. Не представило бы труда определить семантику условных if-then-else выражений в РЕФАЛе, а затем использовать ее, как она применяется, скажем, в Паскале. Можно было бы принять решение об использовании T и F в качестве значений истинности, и определить функцию If в формате:
<If e.Condition Then (e.If-True) Else (e.If-False)>
Когда используется If , активное выражение, вычисляющее значение истинности условия, должно быть подставлено вместо e.Condition . Затем If можно было бы просто определить как:
If {
T Then (e1) Else (e2) = e1;
F Then (e1) Else (e2) = e2; }
Логические связки можно было бы применять подобным же образом. Конъюнкция, например, могла бы быть определена посредством функции And :
And {
T sX = sX;
F sX = F; }
Однако, такой подход приводит к излишним дублированиям. Это будет продемонстрировано на примере процедуры, которая упорядочивает и сцепляет строки.
Предположим, имеется некоторое отношение предшествования (порядка), заданное на строках символов посредством предиката
<Pre (e1)(e2)>
который принимает значение T, если строка e1 предшествует строке e2 , и F в противном случае. Можно определить функцию Order, которая сцепляет две строки в правильном порядке, следующим образом:
Order {
(e1)e2 = <If (<Pre (e1)(e2)>)
Then (e1 e2)
Else (e2 e1)>; }
Пока, при такой интерпретирующей реализации РЕФАЛа, как наша, эта программа не является наилучшим решением. Каждая из переменных e1 и e2 появляется один раз в левой части и три раза в правой части. Это означает, что в ходе выполнения будет создано по две копии каждой строки; если первоначальное выражение сохраняется для вывода, то одна из копий будет использована при вычислении предиката Pre , а другая будет всегда пропадать, так как машина использует только одно из двух выражений для двух значений истинности.
Исключим сперва вопиющую неэффективность создания двух копий (в then- и else-фрагментах), когда нам известно, что только одна из них будет использована на самом деле. Чтобы это проделать, разъединим фрагменты, помещая их в различные предложения. Order вызывает предикат Pre и передает результат, вместе с исходными строками, на вход вспомогательной функции Order1 , которая имеет два предложения для двух фрагментов и осуществляет выбор одного из них (более элегантный способ определения Order без вспомогательной функции будет продемонстрирован в следующей главе, когда будет введено расширение базисного РЕФАЛа):
Order { (e1)e2 = <Order1 <Pre (e1)(e2)>(e1)e2> }
Order1 {
T (e1)e2 = e1 e2;
F (e1)e2 = e2 e1; };
Вместо определения ветвления в алгоритме посредством функции If , или какой-либо другой специальной функции, используем тип ветвления, встроенный в наш язык: выбор предложения в зависимости от аргумента. Функция Pre добавляет к аргументу Order1 индикатор, T либо F , посылая Order1 сигнал, в котором она нуждается для того, чтобы сделать выбор. Этот вид ветвления в РЕФАЛе является и более естественным, и более эффективным. Он также не ограничивает количество альтернатив двумя, но действует как устройство, известное в других языках программирования как переключатель, или как case-выражение.
Наше определение Order потребует создания только одной копии переменных e1 и e2 . Должны ли мы пытаться исключить и это копирование?
Это зависит от ожидаемого размера подобных выражений (и, конечно, от того, насколько часто предполагается вычислять эту функцию). Допустим, e1 и e2 являются английскими словами, а Pre основывается на лексикографическом порядке. Чтобы определить Pre , мы должны сперва задать отношение предшествования в алфавите Pre-alph для букв. В базисном РЕФАЛе это можно проделать следующим образом:
Pre-alph {
*1.This relation is reflexive
s1 s1 = T;
*2.If the letters are different, see whether the
* first is before the second in the alphabet
s1 s2 = <Before s1 s2 In <Alphabet>>; }
Before {
s1 s2 In eA s1 eB s2 eC = T;
eZ = F; }
Alphabet { = 'abcdefghijklmnopqrstuvwxyz'; }
Теперь не представляет труда определить лексикографический предикат Pre :
Pre {
()(e2) = T;
(e1)() = F;
(s1 eX)(s1 eY) = <Pre (eX)(eY)>;
(s1 eX)(s2 eY) = <Pre-alph s1 s2>;
}
Так как длины английских слов невелики, их копирование не приводит к существенной потере эффективности. Это оправдано благодаря простому и естественному определению предиката Pre . Однако в некоторых случаях может быть желательно избегать копирования. Например, если строки состоят не из английских букв, а из некоторых выражений, которые могут быть очень велики, хотелось бы переопределить Pre так, чтобы не производилось ни одного лишнего копирования.
Причиной, почему следует копировать e1 и e2 в определении Order, является то, что Pre ликвидирует свои аргументы и замещает их единственным символом: значением истинности. Таким образом, может быть сформулировано следующее общее правило:
Для того, чтобы избежать неоправданного
дублирования аргументов, следует избегать
неоправданного уничтожения аргументов.
Будем рассматривать такие функции, которые не уничтожают свои аргументы, а просто добавляют к ним T или F, как сохраняющие предикаты. Если вместо Pre используется сохраняющий предикат Prec , функция Order может быть переопределена как
Order { (e1)(e2) = <Order1 <Prec (e1)(e2)>; }
Допустим теперь, что формат Prec определен таким комментарием:
* <Prec (e1)(e2)> == T(e1)(e2) * == F(e1)(e2)
Для того, чтобы определить Prec, модифицируем определение Pre в двух пунктах. Во-первых, обобщаем его до обработки термов вместо простых символов, и заменяем Pre-alph на Pre-term . Во-вторых, новый предикат должен стать сохраняющим. Этого можно достичь, не изменяя формата аргумента. Изменения очевидны для предложений 1, 2 и 4. Но в случае, который соответствует предложению 3, следует хранить первый терм, который является общим для обоих аргументов, для того, чтобы добавить его к ним обоим после того, как предшествование установлено. Решением является:
Prec {
()(e2) = T()(e2);
(e1)() = F(e1)();
(t1 eX)(t1 eY) = <Add-c t1 <Prec (eX)(eY)>>;
(t1 eX)(t2 eY) =
<Pre-term t1 t2>(t1 eX)(t2 eY); }
Add-c { t1 sT(eX)(eY) = sT(t1 eX)(t1 eY); }
Упражнение 3.6 Решение, предложенное выше, не
самое лучшее. Запустите
<Prec ('but')('butter')>
с Pre-alph как Pre-term чтобы увидеть, как он сработает. Предполагая, что длина общего начала двух строк равна c, а верхняя граница количества шагов для вычисления Pre-term равна t, определить количество шагов, необходимое для вычисления Prec . Переопределить его так, чтобы он работал быстрее. Указание: добавить один или более ящиков к формату Prec для накопления общей части. Определить количество шагов, которое потребуется при этом определении.
Как упоминалось выше, не всегда необходимо избегать дублирования. Иногда оно является частью алгоритма. Если это и не так, дублирование часто не приводит к существенной потере эффективности. Например, если алгоритм включает просмотр выражения по одному символу за шаг РЕФАЛ-машины, дополнительное дублирование этого выражения ненамного увеличит время выполнения. Дублирование символов или коротких выражений никогда не было проблемой. Дублирование громоздких выражений на верхнем уровне алгоритма также обычно не составит труда, так как время, в основном, уходит на внутренние циклы. Наконец, более изощренные реализации РЕФАЛа, которые разрабатываются в настоящее время, используют указатели для избежания ненужного копирования.
Пока, программируя для РЕФАЛ-интерпретатора,
следует думать о свободных переменных не как об
указателях на значения, которые где-то размещены,
но скорее как о самих значениях. Когда элементы
левой части переставляются или размножаются, в
правой части предложения этот процесс будет
повторен во время выполнения. Недозволенного
копирования переменных следует решительно
избегать.
Упражнение 3.7 Определить следующие
сохраняющие предикаты:
(a) <String eX> , истинен тогда и только
тогда. когда eX является строкой
(бесскобочной).
(b) <Pal eX> , истинен тогда и только тогда,
когда eX является палиндромом.
3.5. ВСТРАИВАНИЕ АЛГОРИТМОВ В ФУНКЦИИ
Алгоритм на РЕФАЛе является набором функций. Для того, чтобы определить функцию, рассматриваются различные варианты ее аргумента и записываются соответствующие предложения. Таким вот образом функциональные определения встраиваются в предложения. А как некоторый алгоритм встраивается в функции? Далее следует краткое изложение обычных обоснований для введения новой функции, которая рассматривается как алгоритм.
1.ПОСЛЕДОВАТЕЛЬНАЯ ОБРАБОТКА
Когда операция, которую мы хотим выполнить над объектом, может быть определена как последовательное выполнение нескольких операций, мы определяем каждую из операций соответствующей функцией, например:
F { eX = <F3 <F2 <F1 eX>>> }
Здесь результат одной функции становится аргументом для другой.
1.ПАРАЛЛЕЛЬНАЯ ОБРАБОТКА
Когда различные части объекта должны подвергнуться обработке по отдельности, мы определяем функции, которые применяются к соответствующим частям, например:
F { (eX)(eY)eZ = <F1 eX> <F2 eY> <F3 eZ> }
3.РАЗБИЕНИЕ ВЫРАЖЕНИЯ НА ЧАСТИ
В результате выполнения предыдущих шагов мы можем получить структурированный объект, различные части которого подразумевают различные применения. Например, функция деления нацело </ s.N1 s.N2> продуцирует комбинацию (s.Quotient)s.Remainder . Если нам нужен только остаток от деления s.N1 на s.N2 , мы вызываем:
<Rem </ s.N1 s.N2>>
где Rem определяется предложением:
Rem { (sQ) eR> = eR }
4.ВЕТВЛЕНИЕ ПО
ЗНАЧЕНИЮ ФУНКЦИИ
Часто возникает потребность вычислить некоторую функцию F , а затем, в зависимости от результата вычисления, продолжать вычисления тем или иным путем. Тогда мы вводим вспомогательную функцию F1 , и производим вызов:
<F1 <F eX>>
Функция ветвления F1 анализирует результат F и производит требуемый выбор. Мы уже видели многие примеры этого.
5.ИЗМЕНЕНИЕ ФОРМАТА
Часто требуются дополнительные подаргументы функции для того, чтобы определить рекурсивный процесс. В этом случае определяется вспомогательная функция с требуемым форматом. В приведенном выше примере было видно, что мы определили функцию Cor с форматом:
<Cor (e.Scanned-already) e.Not-yet-scanned>
для того, чтобы определить функцию Correct :
Correct {
e1 = <Cor () e1>; }
Взаимодействие между функциями в РЕФАЛ-системе может производиться либо через поле зрения, либо посредством прямых вызовов. В примере последовательной обработки, приведенном выше:
F {eX = <F3 <F2 <F1 eX>>> }
мы использовали взаимодействие через поле зрения. Каждая из трех функций, F1 и т.д., ничего не знает о других. Она оставляет свое значение в поле зрения, а следующая функция принимает его. Альтернативой этому является определение F через систему прямых вызовов. F сама просто вызывает F1 :
F { eX = <F1 eX> }
Определение F1 теперь должно быть модифицировано. В нерекурсивных предложениях, где прежнее определение F1 заканчивало работу с выражением в качестве результата, новое определение должно оканчиваться <F2_.> . Определение F2 должно быть модифицировано таким же образом.
Взаимодействие через поле зрения имеет то преимущество, что функциональные определения независимы от их применения, так что они могут быть использованы также и в других контекстах. Итак, по этому методу мы можем надстраивать результат функции справа в поле зрения, например, по схеме, которая уже использовалась (см. функции Chpm , Blanks , и т.д.):
F {... = Е <F ...> }
где Е есть некоторое выражение. Эта схема может варьироваться:
F {... = <F ...> Е }
или
F {... = Е1(<F ...>)Е2 }
и т.д. При прямом вызове функций-преемников это невозможно. С другой стороны, прямые вызовы удобны, когда функция имеет различных преемников в различных предложениях.
В программировании термин рекурсия имеет специальное значение и часто противопоставляется итерации. Рекурсия и итерация являются двумя основными способами определения циклических процессов. Сравним их, взяв в качестве примера функцию факториал и используя в качестве языка программирования Паскаль. Итеративным определением является:
function fact(n:integer):integer; var f:integer; begin f := 1; while n > 0 do begin f := n * f; n := n - 1 end; fact := f end
Здесь заголовок сообщает нам, что fact является функцией целочисленной переменной; n является формальным параметром. Еще одна целочисленная переменная, f , используется при вычислении. Вначале она принимает значение 1. Затем включается проверка, превосходит ли n значение 0. До тех пор, пока это не выполняется, вычисляются новые значения f и n, а управление возвращается на проверку условия. Это простой цикл с двумя переменными, изменяющими свое значение в ходе вычислений.
Сравним это с рекурсивным определением той же самой функции:
function fact(n:integer):integer; begin if n = 0 then fact := 1 else fact := n * fact(n-1) end
Когда выполняется эта программа, аргумент n сперва сравнивается с 0. Если он не является 0 (и подразумевается, что он неотрицателен), то n должно быть умножено на значение той же самой функции fact для меньшего аргумента n-1 . Это означает, что вычисление вычисления первоначального функционального вызова должно быть приостановлено и fact(n-1) должно быть вычислено посредством той же программы. Текущее значение n и fact (хотя последнее и не будет использоваться на самом деле) должны быть сохранены в памяти для продолжения вычислений fact(n) после того, как будет вычислено fact(n-1). Эта процедура откладывания будет повторена n раз, пока текущее значение n не станет равным 0. Затем отложенные вызовы возобновляются и выполняются в обратном порядке так, что наконец мы приходим к ответу. Говорят, что отложенные вызовы функции в процессе рекурсивного вычисления образуют стэк (они размещаются один над другим, а используются в обратной последовательности). Таким образом, перед тем, как числа действительно начинают перемножаться, следует запомнить 2n чисел. К тому же следует организовать правильное возобновление отложенных вызовов функции. Очевидно, что рекурсивное вычисление более сложно и требует больше времени и компьютерной памяти, чем итеративное.
РЕФАЛ-функция является рекурсивной, если она вызывает себя самое непосредственно или в результате последовательности вызовов других функций. Но рекурсия в этом смысле не обязательно означает рекурсивность в терминах Паскаля. Это отличие проистекает из отличий в семантике функционального вызова. В Паскале, когда функция сама себя вызывает, она откладывает выполнение программы, чтобы вернуться к нему позднее. В РЕФАЛе же правая часть предложения замещает вызов функции. Если функция вызывает сама себя с другим аргументом:
F {... = <F ...> }
это, в терминах Паскаля, является итерацией, но не рекурсией: вызов функции воспроизводит сам себя, изменяется только аргумент. Когда управляющая структура имеет вид:
F1 { ... = <F1 ...<F2 ...>...> }
либо
F1 ... = <F2 ...> <F1 ...>
это снова является присущим 'Паскаль-итерации', но не 'Паскаль-рекурсии'. Вызов F2 вычисляется первым, и снова имеется единственный функциональный вызов F1 . Не происходит никакого накопления вызовов в поле зрения.
Настоящая 'Паскаль-рекурсия' возникает за счет структур следующего вида:
F1 {... = <F2 ...<F1 ...>...> }
либо
F1 {... = <F1 ...> <F2 ...> }
В РЕФАЛе не существует прерываемых, или отложенных, вызовов функций, так как работа РЕФАЛ-машины состоит просто из последовательности замещений. Но функциональный вызов, как единое целое, может ожидать своей очереди в поле зрения. Вот что происходит с вызовами F2 : они накапливаются в поле зрения, подобно отложенным вызовам Паскаль-функции fact .
Ранее уже представлялся случай продемонстрировать рекурсивное определение факториала в терминах РЕФАЛа:
Fact {
0 = 1;
sN = <* sN <Fact <- sN 1>>>; }
Когда вычисляется <Fact 10> , первые 20 шагов порождают структуру:
<* 10 <* 9 ... <* 1 <Fact 0>> ... >>
затем работает первое предложение из определения Fact, и десять последующих шагов умножения приводят к результату. Это весьма похоже на случай Паскаль-функции, но отсроченные вызовы обозначены * , а не Fact .
Можно переопределить Fact в виде итерации, полностью аналогично Паскаль-определению. Функция, которая будет выполнять работу, должна будет включать все переменные, используемые в цикле, а именно переменную цикла s.n , которая первоначально является такой же, как аргумент, и накапливаемый результат s.f , который первоначально равен 1. Первым шагом поэтому будет преобразование формата:
Fact { s.n = <Loop s.n 1>; };
Здесь нет ничего, кроме присваивания начальных значений переменным цикла. Сам цикл определяется следующим образом:
Loop {
*1.Termination condition satisfied
0 s.f = s.f;
*2.Otherwise
s.n s.f = <Loop <- s.n 1> <* s.n s.f>>; }
Функциональные определения такого типа, каким задается Loop, известны под названием остаточная рекурсия. В функциях этого вида расширение функционального вызова включает не более одного рекурсивного вызова функции, и, коль скоро он имел место, он должен быть последней операцией в расширении. Из-за этого остаточно-рекурсивные функции допускают реализацию, которая является итеративной, т.е. исключает накопление отсроченных вызовов функций. Трансляторы для Паскаля и для других универсальных языков не используют эту возможность и транслируют остаточно-рекурсивные функциональные определения таким же образом, как и общие рекурсивные определения. Это также справедливо для ранних реализаций Лиспа. В самой последней реализации Лиспа и ее версиях (например, Scheme) позаботились о реализации остаточной рекурсии в форме итерации. В РЕФАЛе нет нужды уделять специальное внимание остаточной рекурсии: подобные определения исполняются итеративно в силу самой семантики языка.
Итеративные (остаточно-рекурсивные) определения используют память экономно, в то время как 'по-настоящему рекурсивные' определения могут породить громадные промежуточные структуры в поле зрения. Но с другой стороны рекурсивные определения, как правило, короче и более прозрачны.
Рассмотрим характер рекурсии на примере очень простой функции обработки строк, которая трансформирует каждое A в B :
Fab {
A e1 = B <Fab e1>;
s2 e1 = s2 <Fab e1>;
= ; }
Будучи написанным и исполняемым в РЕФАЛе, это определение является итеративным. В самом деле, расширение вызова функции включает не более одного функционального вызова; символы накапливаются в поле зрения как части окончательного результата, а накопления функциональных вызовов не происходит. И все же само определение рекурсивно по форме, а не итеративно. Если записать полностью аналогичное определение в Лиспе:
(define (fab x) (cond ((null x) nil) ((equal (car x)(quote a)) (cons (quote b) (fab (cdr x)))) (T (cons (car x)(fab (cdr x)))) ))
то оно определенно является рекурсивным, но не остаточно-рекурсивным: отложенные вызовы функции-конструктора cons накапливаются в памяти до тех пор, пока значение аргумента функции fab не становится равным nil (пустым). Различие проистекает из разных способов трактовки основных операций над строками и выражениями, т.е. сопоставления с образцом и подстановки. В РЕФАЛе эти операции являются частью встроенного кибернетического механизма, который трактует их как физические объекты. Обрабатываемые символы (либо громоздкие выражения в иных случаях) накапливаются в соответствующих местах поля зрения по мере поступления, и нет необходимости откладывать какие-либо вызовы функций. При таком способе ясность и краткость рекурсивного определения сочетаются с эффективностью итеративного определения. Если необходимо использовать специальный конструктор Cons для конкатенации (сцепления) термов в левой части выражения, как в случае Лиспа, наше выражение могло бы быть 'по-лисповски рекурсивным':
Fab {
A e1 = <Cons B <Fab e1>>;
s2 e1 = <Cons s2 <Fab e1>>;
= ; }
что приводит к накоплению отложенных вызовов функции.
Легко переписать первое определение Fab в классической остаточно-рекурсивной (итеративной) форме:
Fab {e1 = <Fab1 ()e1>; }
Fab1 {
(e1) A e2 = <Fab1 (e1 B) e2>;
(e1) s3 e2 = <Fab1 (e1 s3) e2>;
(e1) = e1; }
Но нельзя то же самое проделать в Лиспе (до тех
пор, пока его структуры данных не будут расширены
за счет включения специальных функций для
обработки строк). Как видно из первых двух
примеров задания Fab1 , последний
обрабатываемый символ должен быть добавлен справа
к текущему результату трансформации e1 .
В Лиспе же cons добавляет терм к списку
только слева: либо необходимо использовать
функцию append (которая совершенно
неэффективна), либо конструировать строку в
обратном порядке, а затем реверсировать ее,
приводя к первоначальному виду (что удваивает
время выполнения).
Упражнение 3.8 Функция факториал может быть
вычислена перемножением чисел в порядке
возрастания. Определить РЕФАЛ-функцию, которая
использует этот алгоритм.
Упражнение 3.9 Определить функцию Reverse,
которая переписывает строку в обратном порядке
(реверсирует), как рекурсивным, так и итеративным
способами. Проанализировать, как они ведут себя в
смысле времени выполнения. Какое определение
предпочтительнее?
3.7. РАБОТА С ВЛОЖЕННЫМИ СКОБКАМИ
В РЕФАЛе отношение к скобкам весьма серьезно. Ни при каких обстоятельствах нельзя трактовать их как символы (разумеется, это не распространяется на символы '(' и ')' , которые ничем не отличаются от остальных символов). Выражение представляет собой дерево, в котором символы являются листьями, а заключенные в скобки термы - поддеревьями. Если мы захотим, например, заменить '+' на '-' на всех скобочных уровнях, мы сможем проделать это только при точном определении процесса расстановки вложенных скобок. Простейшее решение таково:
* Change every '+' to '-', depth-first order.
Chpm {
'+'e1 = '-'<Chpm e1>;
sX e1 = sX <Chpm e1>;
(e1)e2 = (<Chpm e1>) <Chpm e2>;
= ; }
Этот способ обработки деревьев известен как метод "внутри-слева". Всякий раз, когда встречается поддерево, т.е., мы натыкаемся на левую скобку, сперва производится переход вниз (внутрь), как предписывает первый вызов Chpm в предложении 3, и только после того как полностью обработано это поддерево, производится второй вызов функции.
Вот другой способ подробного определения Chpm :
* Change every '+' to '-' using open e-variables
Chpm {
e1 '+' e2 = <Chpm-d e1> '-' <Chpm e2>;
e1 = <Chpm-d e1>; }
* Go down with Chpm
Chpm-d {
e1 (e2) e3 = e1 (<Chpm e2>) <Chpm-d e3>;
e1 = e1; }
Теперь порядок, в котором обрабатывается аргумент, иной.
Когда длинное выражение просто выдается на печать построчно, его может быть трудно прочесть. Желательно написать процедуру ( "красивой печати''), которая распечатывала бы выражение в более читабельной форме. Точнее говоря, желательно, чтобы все скобки были напечатаны в отдельных строках с отступом, пропорциональным структурному уровню терма. Поэтому правые скобки следовало бы печатать в той же колонке, что и сопряженные им левые скобки.
Следующая далее программа решает эту проблему. Идея ее состоит в том, чтобы хранить строку пробелов как отступ и удлинять ее при входе в новый скобочный уровень.
* Pretty print-out of expressions
$ENTRY Pprout { eX = <Pprt (' ') eX>; }
/* Initial offset 1 to see transfers */
* <Pprt (e.Blanks-offset) e.Expression>
Pprt {
(eB) e1(e2)e3 = <Pr-ne (eB) e1>
<Prout eB'('>
<Pprt (eB' ') e2>
<Prout eB')'>
<Pprt (eB) e3>;
(eB) e1 = <Pr-ne (eB) e1>; }
* Print if non-empty
Pr-ne {
(eB) = ;
(eB) e1 = <Prout eB e1>; }
Если на вход Pprout поступает следующее выражение :
'000'('111111')'00000'(('222')'111111')'0000'
то оно будет распечатано таким образом:
000 ( 111111 ) 00000 ( ( 222 ) 111111 ) 0000
Упражнение 3.10 Функция Pprout ,
определенная выше, использует целую строку для
каждой скобки. Распечатка может быть несколько
сжата, если левая скобка не вызывает появления
новой строки:
000 (111111 ) 00000 ((222 ) 111111 ) 0000
Переопределить Pprout так, чтобы распечатывать выражения указанным образом.
Функция Chpm, определенная выше, может применяться независимо к отдельным ветвям дерева. Такие функции особенно легко определять с помощью рекурсии. Однако часто деревья обрабатываются таким образом, что информация передается от одной ветви к другой. Например, мы могли бы захотеть обойти дерево при поиске "внутри-слева" и сохранить только те листья, которые появляются только первый раз. Для этой цели нам необходим указатель, который продвигается по дереву, т.е., проходит все структурные уровни выражения.
Некоторый опыт работы с указателями в РЕФАЛе уже приобретен. Когда обрабатывается строка, положение указателя может быть представлено парой скобок; используется
( 'ABCDEF' ) 'GHIJKLM'
вместо
'ABCDEF' ^'GHIJKLM'
Если бы требовалось применять Chpm только к строкам, можно было бы определить ее как использующую указатель вместо накопления результата в поле зрения:
* Change every '+' to '-' in a string
Chpm { e1 = <Chpm1 ()e1>; }
/* set pointer at the beginning */
Chpm1 {
(e1) '+'e2 = <Chpm1 (e1'-') e2>;
/* move pointer and replace +*/
(e1) sX e2 = <Chpm1 (e1 sX) e2>;
/* move pointer */
(e1) = e1;
/* end of work */
}
В такой форме наше определение можно модифицировать, чтобы организовать использование в трансформации обеих частей строки. Предположим, например, что '+' не просто замещается на '-' , но замещается на всю предшествующую строку, таким образом дублируя ее (вообще-то глупая вещь, но достаточно хорошая в качестве иллюстрации). Тогда первое предложение для Chpm1 должно быть переписано как:
(e1) '+'e2 = <Chpm1 (e1 e1) e2>;
Мы могли бы не делать этого, если бы результат накапливался в поле зрения.
Но что делать, если мы обрабатываем выражение и хотим использовать указатель внутри скобок? Рассмотрим, например, такое размеченное выражение, т.е. выражение с указателем:
'AB'('C'('DEF' ^'GH')'KLM'('V')'XY')
Часть выражения, которая предшествует указателю, сама не является выражением и не может быть заключена в скобки. То же справедливо и для части, следующей за указателем. Назовем эти части мультискобками, левой и правой соответственно. Можно принять соглашение о представлении мультискобок с помощью выражений. Имеются два естественных представления: с последовательными либо вложенными форматными скобками. Обсудим подробно последовательное представление, которое более наглядно и легче для употребления.
В левой мультискобке некоторое количество непарных скобок разделяет выражение на n сегментов. В правой мультискобке существует в точности то же количество n сегментов, разделенных правыми скобками. Для того, чтобы представить мультискобку выражением, каждый сегмент заключается в пару скобок. Для левой мультискобки:
Е1(Е2(... (Еn ==>(Е1)(Е2)(...)(Еn)
Для правой мультискобки:
Е1)Е2)...)Еn ==>(Е1)(Е2)(...)(Еn)
Размеченное выражение, упомянутое выше, принимает вид:
('AB')('C')('DEF') ^('GH')('KLM'('V')'XY')()
Теперь можно заменить указатель еще одной парой скобок, и это будет окончательным представлением размеченных выражений:
01 11 11 1 0 1 11 2 2 111
(('AB')('C')('DEF') ) ('GH')('KLM'('V')'XY')()
Пара скобок, представляющих указатель, помечена уровнем 0; все другие скобки помечаются, начиная с 1 и игнорируя указательные скобки. Скобки, имеющие уровень 1, являются форматными для мультискобки; все остальные являются первоначальными скобками исходных выражений. Для прочтения мультискобочного представления исходного размеченного выражения, производятся следующие действия:
01 1
1.Игнорировать (( слева, и ) справа.
101
2.Читать ))( как указатель.
11
3.Читать )( слева/справа от указателя
как непарную левую/правую скобку
в левой/правой мультискобке.
Теперь остается только сделать последний шаг для удобства применения мультискобочного формата. Примем e.ML и e.MR в качестве стандартных переменных для заключающих левой и правой мультискобок, и введем следующие обозначения:
[ stands for (e.ML ( ] stands for )e.MR [. stands for (( .] stands for ) ^ stands for ))(
Эта таблица должна сопровождаться толкованием, что внутри квадратных скобок каждая 'непарная' круглая скобка, т.е., та, для которой ее пара расположена по другую сторону указателя, заменена инвертированной парой )( .
При такой системе обозначений размеченные мультискобочные выражения представляются наиболее естественным образом. Размеченное выражение, рассмотренное выше, приобретает вид:
[.'AB'('C'('DEF' ^'GH')'KLM'('V')'XY').]
Единственным дополнением к простому введению указателя в нужной позиции является заключение всего выражения в квадратные скобки с точками.
Квадратные скобки без точек используются при записи предложений в мультискобочном формате. Предложение, согласно которому функция F перемещает указатель на одну позицию вправо, имеет вид:
[ e1 ^ sX e2 ] = <F [ e1 sX ^ e2 ]>;
Предложение для входа в левую скобку имеет вид:
[ e1 ^ (e2)e3 ] = <F [ e1 ( ^ e2)e3 ]>;
Вот каким образом это соответствует действительному предложению:
[ e1 ^ (e2)e3 ] = (e.ML( e1 ))( (e2)e3 )e.MR = [ e1 ( ^ e2 ) e3 ] (e.ML( e1 )( ))( e2 )( e3 )e.MR
Чтобы транслировать предложение в мультискобочном формате в обычное предложение, используется приведенная выше таблица и производится замещение непарных скобок на инвертированные пары )( . Повторяющиеся квадратные скобки употребляются для специального случая, когда мультискобочные переменные e.ML и e.MR являются пустыми; это применяется для вызова и закрытия функций, использующих мультискобочный формат. Предложение, которое запускает мультискобочную обработку некоторого выражения e1, помещая указатель перед ним, имеет вид:
e1 = <F [. ^ e1 .]>;
Стоит упомянуть о следующем правиле: когда e.ML и e.MR составляют выражение, количество термов в них обеих должно быть одинаковым. Однако, в процессе формирования нового выражения (как в следующем далее случае функции Pair ) e.ML и e.MR могут и не удовлетворять такому отношению.
Эта система обозначений реализована не как расширение базисного РЕФАЛа. Она используется как макро-нотация. Программы, ее использующие, должны транслироваться, вручную либо автоматически, в регулярный РЕФАЛ так, чтобы, когда программист реально использует РЕФАЛ-программу, он смог видеть транслированные предложения такими, какими они действительно используются в РЕФАЛ-машине. Обоснование такого подхода кроется главным образом в том, что следует принимать во внимание отладку. В некоторых случаях нам также может захотеться работать непосредственно с представлениями мультискобок.
Полностью функцию Chpm можно определить, при использовании мультискобочной техники, следующим образом:
Chpm { e1 = <Chpm1 [. ^ e1 .]>; }
/* change to MB format;
set pointer at the beginning */
Chpm1 {
[ e1 ^ '+' e2 ] = <Chpm1 [ e1'-' ^ e2 ]>;
[ e1 ^ sX e2 ] = <Chpm1 [ e1 sX ^ e2 ]>;
[ e1 ^ (e2)e3 ] = <Chpm1 [ e1( ^ e2)e3 ]>;
[ e1(e2 ^ )e3 ] = <Chpm1 [ e1(e2) ^ e3 ]>;
[. e1 ^ .] = e1; }
Этот текст должен быть странслирован в регулярный РЕФАЛ. РЕФАЛ-система включает функцию Mbprep (мультискобочный препроцессор), написанную на РЕФАЛе. Она обнаруживает те предложения в программе, которые используют макро-нотацию, и транслирует их. Когда Mbprep.rsl находится в Вашей текущей директории, запустите
refgo mbprep source-file out-file
Предложения, использующие мультискобочную макро-нотацию, гораздо легче читать, чем действительные предложения, которые они замещают. Хорошей практикой является переписывание таких предложений в терминах макро-нотации и сохранение их в окончательной программе в форме комментариев. Просто сделайте копию каждого такого предложения и добавьте звездочку в начале каждой строки. Затем вызовите Mbprep .
Продемонстрируем результат на примере функции Pair . Базовые функции чтения РЕФАЛ-5 порождают РЕФАЛ-выражения, состоящие только из набираемых символов. Если мы хотим конвертировать символы '(' и ')'в таких выражениях в "настоящие'' скобки РЕФАЛа, можно использовать функцию, определенную следующим образом:
*** Function Pair pairs symbol-parentheses
$ENTRY Pair{
* eX = <Pair1 [. ^ eX .]>
eX = <Pair1 (( ))( eX )> };
Pair1 {
* [ e1 ^ '('e2 ] = <Pair1 [ e1( ^ e2 ]>;
(e.ML( e1 ))( '('e2 )e.MR =
<Pair1 (e.ML( e1)( ))( e2 )e.MR>;
* [ e1(e2 ^ ')'e3 ] =
* <Pair1 [ e1(e2) ^ e3 ]>;
(e.ML( e1)(e2 ))( ')'e3 )e.MR =
<Pair1 (e.ML( e1(e2) ))( e3 )e.MR>;
* [. e1 ^ ')'e3 ] = error message;
(( e1 ))( ')'e3 )e.MR =
<Prout "*** ERROR: Unpaired ')' found:">
<Prout '*** 'e1')'>;
* [ e1 ^ s2 e3 ] = <Pair1 [ e1 s2 ^ e3 ]>;
(e.ML( e1 ))( s2 e3 )e.MR =
<Pair1 (e.ML( e1 s2 ))( e3 )e.MR>;
* [. e1 ^ .] = e1;
(( e1 ))( ) = e1;
* [ e1 ^ .] = error message;
(e.ML( e1 ))( ) =
<Prout "*** ERROR: Unbalanced '(' found:">
<Pr-lmb e.ML>; }
* PRint Left MultiBracket
Pr-lmb {
(e1)e2 = <Prout '*** 'e1'('> <Pr-lmb e2>;
= ; }
Когда программа встречает правую скобку, которая не имеет пары, предшествующее выражение уже не имеет мультискобок, так что оно просто выдается на печать, чтобы локализовать ошибку. Когда обработка доходит до конца выражения и имеется непарная левая скобка, просмотренная часть выражения все еще в мультискобочном формате, поэтому вводится Pr-lmb для того, чтобы выдать ее на печать.
Интересной особенностью последовательного мультискобочного формата является то, что при обработке дерева весь путь от указателя до корня дерева представлен в виде последовательности термов и потому легко доступен. Прибегнем к представлению деревьев в форме РЕФАЛ-выражений, используя следующие правила:
Так, дерево на Рис. 3.1 записывается в форме:
T(A(B.C.)D(E.F(G.H.I.)J.)K.)
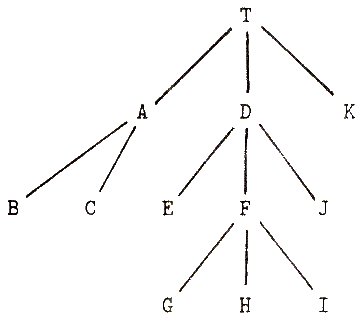
Рисунок 3.1 Дерево объектов
Если только что пройден H , размеченное дерево в мультискобочной макро-нотации будет иметь вид:
[.T(A(B.C.)D(E.F(G.H ^ .I.)J.)K.).]
что соответствует:
( (T)(A(B.C.)D)(E.F)(G.H) ) (.I.)(J.)(K.)()
(Заметим, что если бы этот текст был частью программы, все данные-точки стояли бы в кавычках, отличаясь таким образом от точек, используемых при квадратных скобках, которые, конечно, в кавычки не заключаются.)
Здесь можно отследить пути от текущего пункта во всех четырех направлениях: вперед, назад, вверх или вниз. Если восстанавливается путь от указателя ( 0- уровень скобок) назад, видно, что последним пройденным объектом был H ; также можно далее увидеть на предшествующей ветви лист G. , являющийся братом H . Для того, чтобы подняться вверх по дереву, продвигаемся на один мультискобочный терм влево и видим, что предком H является F . Уровнем выше мы видим D как более отдаленного предка, а затем T . В РЕФАЛ-выражении все эти объекты находятся в одинаковой позиции: последний объект внутри терма первого уровня. Остальные объекты, такие как A , находятся вне пути. Их форма сохранена: взятие в мультискобки оставляет их в стороне.
Из-за этого свойства мультискобочного формата можно работать с путем от корня дерева до текущего пункта, используя открытые переменные. Предположим, например, для таких деревьев, как описано выше, мы хотим определить функцию, которая определяла бы, находится ли объект sX на пути к указанному узлу. Пусть форматом функции является:
<In-path sX e.Tree>
Для выполнения этой работы вводится следующее определение :
In-path {
sX (e1(e.Sibl sX)e2) e3 = True;
eZ = False; }
Здесь e.Sibl является списком уже
просмотренных братьев узла sX .
ЗАМЕЧАНИЕ: Указанный метод является общим
методом записи функций, которые используют
мультискобки. Сперва описывается ситуация в
естественной форме, с использованием примера или
схемы, и определяется необходимая трансформация
в этих терминах. Далее можно следовать по одному
из двух путей; какой-либо из них, возможно,
окажется более полезным, чем другой. Можно прямо
выразить трансформацию в мультискобочном
формате и затем использовать mbprep . Либо
сперва транслировать трансформационную схему в
мультискобочный формат, а затем записать
соответствующие РЕФАЛ-предложения.
Упражнение 3.11 Иногда необходимо прекратить
мультискобочную обработку и выдать выражение в
том виде, который оно имеет в текущий момент.
Тогда мы должны провести обратную трансформацию
мультискобочного представления в регулярное
РЕФАЛ-выражение, которое стоит за ним. Записать
функцию Mback, осуществляющую это.
Упражнение 3.12
(a) Пусть дана функция <Subtree sX>, которая
конвертирует узел sX в поддерево,
начинающееся с корня sX. Предполагается,
что функция Subtree будет использоваться
рекурсивно, т.е. нелистовые узлы, возникающие в
результате Subtree , еще потребуют
повторного применения этой функции. Определить
функцию Tree , которая будет строить
полное дерево по данному корневому узлу.
(b) Если Subtree требует большого времени для
вычисления, может быть полезным просмотр всего
существующего дерева перед применением этой
функции. Если текущий узел уже перед этим возник,
и его поддерево было определено, тогда оно может
быть скопировано, чтобы не получать его повторно.
Записать модификацию Tree, которая
реализует этот алгоритм.