Рис. 1.1 Дерево для алгебраического выражения
1. БАЗИСНЫЙ РЕФАЛрефал
| 1.1. Определение простой функции |
| 1.2. Символы и выражения |
| 1.3. Сопоставление с образцом |
| 1.4. Предложения и программы |
| 1.5. Абстрактная РЕФАЛ-машина |
| 1.6. Дальнейшие примеры функций |
1.1. ОПРЕДЕЛЕНИЕ ПРОСТОЙ ФУНКЦИИ
Рассмотрим следующую простую задачу. Вы хотите задать функцию, которая определяет для любой заданной строки символов, является ли она палиндромом. Палиндром - это строка, одинаково читаемая как слева направо, так и справа налево. Имеются два очевидных способа уточнить такое определение палиндрома. Первый - это определить процедуру реверсирования строки (записи посимвольно задом наперед), а затем сравнивать реверсированную строку с исходной. Очевидно, алгоритм, создаваемый на основе такого уточнения, будет не самым эффективным . Если строка оканчивается символом, отличным от начального, то она не является палиндромом, а это может быть установлено без реверсирования всей строки. Поэтому мы примем за основу другое уточнение, которое можно записать в обычной математической форме:
1) Пустая строка является палиндромом.
2) Строка из одного символа является палиндромом.
3) Если строка начинается и оканчивается одним и тем же символом, то она является палиндромом тогда и только тогда, когда строка, полученная из нее путем удаления начального и конечного символов, является палиндромом.
4) Если не выполнено ни одно из вышеприведенных условий, строка палиндромом не является.
Пусть Pal - имя функции, которую мы хотим определить, и пусть она принимает значение True в случае, когда ее аргумент - палиндром, и False в противном случае. Определение в РЕФАЛе почти буквально следует математическому определению:
Pal { = True;
s.1 = True;
s.1 e.2 s.1 = <Pal e.2>;
e.1 = False; }
Эта программа начинается с имени функции, за которым следует блок, заключенный в фигурные скобки. Блок - это список предложений, разделяемых точкой с запятой. В нашем случае имеем четыре предложения, каждое из которых соответствует одному пункту в приведенном выше математическом описании палиндрома. Предложение представляет собой правило замены. Его левая часть представляет образец аргумента функции, правая же часть после знака равенства является заменой для вызова функции.
В первом предложении аргумент функции Pal - пустая строка, поэтому значением функции должно быть True .
Во втором предложении аргумент задан как свободная переменная символа s.1 . Этому образцу будет удовлетворять любой символ, например, буква, но только один символ. Таким образом, предложение читается: если аргумент - единственный символ, заменить вызов на True .
Третье предложение представляет случай, когда аргумент начинается и оканчивается одним и тем же символом s.1 , и содержит любое выражение e.2 между ними. Выражение является самой общей структурой данных в РЕФАЛе; в частности, оно может быть строкой символов. Правая часть этого предложения есть вызов функции Pal от аргумента e.2 . Будем использовать круглые скобки для формируемых структур данных, а угловые - для обозначения вызова функции. Записываем <Pal e.2> в случае, который соответствует математическому обозначению pal(e2) .
Наконец, аргументом в последнем предложении является произвольное выражение (строка). Каждое предложение в определении функции в РЕФАЛе применяется только тогда, когда ни одно из предшествующих предложений не было применимо. Таким образом, последнее предложение означает: если ни один из вышерассмотренных случаев не имел места, тогда при любом аргументе значением вызова функции является False .
Точное задание алгоритмической семантики РЕФАЛ-программ дается через определение абстрактной РЕФАЛ-машины (см. Разд. 1.5) , которая выполняет РЕФАЛ-программы, т.е. вычисляет функции, определяемые в РЕФАЛе. РЕФАЛ-машина работает пошагово, причем каждый шаг состоит в выполнении одного предложения. Если, например, мы даем РЕФАЛ-машине вызов Pal с аргументом 'revolver' , т.е. <Pal 'revolver'> , то рабочее пространство РЕФАЛ-машины (которое мы будем называть полем зрения ) проходит через следующие стадии:
<Pal 'revolver'>
<Pal 'evolve'>
<Pal 'volv'>
<Pal 'ol'>
False
Это демонстрирует детальную картину процесса вычисления. Программист может управлять этим процессом с помощью трассировщика. В простейшем случае он может просматривать и выдавать на печать все последовательные стадии процесса, как это было описано выше.
Теперь начнем систематическое определение РЕФАЛа. Краткое описание синтаксиса языка приведено также в Разделе справочника B.
Символ в РЕФАЛе - это минимальный синтаксический элемент структур данных. Используются следующие виды символов:
Идентификатором является последовательность знаков, которая начинается с заглавной буквы и может включать буквы, цифры, черточки - и подчеркивания _. Размер букв, за исключением первой, не играет роли; так, SUM1 и Sum1 представляют один и тот же идентификатор. Черточки и подчеркивания также взаимозаменяемы: Sum-1 и Sum_1 означают одно и то же. Идентификаторы не должны разделяться пробелами и знаками переноса. Общая длина идентификатора не должна превышать 15 знаков.
Правильными идентификаторами являются:
A X1 Y2g3h56c CrocoDile Hit-and-run
Не являются правильными идентификаторами:
a x1 16x Me+You Input/output
Все печатные знаки компьютерной системы могут использоваться в качестве символов. Чтобы отличать знаки от символов-имен, мы будем заключать первые в кавычки. Для выделения строки знаковых символов будем заключать в кавычки всю строку. Могут использоваться как одинарные ' , так и двойные " кавычки, но открывающая и закрывающая кавычки должны быть одного типа. Таким образом, 'A' есть один символ, в то время как 'A+B' есть строка (последовательность) трех символов: знаков 'A' , '+' и 'B' .
Для представления самих кавычек мы дублируем их, независимо от того, изолированы они или находятся внутри строки, ограничиваемой того же вида кавычками. Так '*,''' является строкой из трех символов: звездочки, запятой и одинарной кавычки. Это может быть также записано как "*,'" .
Односимвольные идентификаторы не следует путать с алфавитными символами: A отличается от'A' . Алфавитные символы разных регистров также различаются: 'A' отлично от 'a' .
Макроцифрами в нашей реализации РЕФАЛа-5 являются положительные целые числа в диапазоне от 0 до 232-1. Превосходящие 232-1 числа могут быть составлены из макроцифр с использованим основания 232 , так же как десятичные целые числа составляются из обычных (десятичных) цифр; этим и объясняется имя "макроцифра". Для представления отрицательных целых чисел мы помещаем '-' перед цифрами, так же, как это делается при использовании десятичных цифр. Подобно буквам алфавита, которые отличаются от букв-идентификаторов, цифры отличаются от числовых символов. '1' - это не то же самое, что 1 . В отличие от первой единицы - обычной десятичной цифры - вторая единица рассматривается как макроцифра.
Примеры: 3306 является символом -- макроцифрой с численным значением 3306 . '-'25 является последовательностью двух символов; за алфавитным символом '-' следует макроцифра 25 . Вместе они будут восприниматься арифметическими функциями как число -25. (В программах все знаки должны заключаться в кавычки; при считывании данных функцией Input [см. Разд.2.3] кавычки не являются обязательными.) В следующем примере:
2543 88918 9
является последовательностью трех макроцифр, которая будет пониматься как
2543*264 + 88918*232 + 9
ЗАМЕЧАНИЕ: Если вы записываете нечто вроде '--'25
, это не будет считаться синтаксической ошибкой.
Это вполне допустимая строка из трех символов.
Ошибочной она станет только тогда, когда вы
попытаетесь использовать такую строку в
качестве операнда в арифметической функции.
Действительное число в языке РЕФАЛ-5 всегда представлено символом, занимающим одно машинное слово. Действительное число может быть положительным, отрицательным или нулем. В программе действительные числа записываются в обычном виде с точкой, отделяющей дробную часть от целой, и с знаком E, отделяющим десятичный порядок. Примеры:
215.73 -18E+15 0.003E-7
(см. в Разделе справочника B более подробный синтаксис). Символы, представляюшие действительные числа, отличаются от макроцифр: 215 - не то же самое, что 215.0 .
Вообще говоря, пробелы не считаются символами; пробелы и символы переноса используются для разделения лексических единиц РЕФАЛа всюду, где это необходимо, и для более удобного размещения их на странице. Единственной ситуацией, когда пробел становится символом, является случай его использования внутри кавычек. Если '' - это символ кавычек, то ' ' - это символ пробела. При использовании между строками, заключенными в кавычки, пробел говорит о том, что снять кавычки можно только с каждой из них по отдельности. Так, 'a' 'b' является строкой из двух символов, a и b , в то время как 'a''b' - это строка из трех символов: a , кавычки и b.
Для создания структур данных в РЕФАЛе используются скобки. Не заключаемые в кавычки круглые скобки - это не символы, но специальные знаки РЕФАЛа. Мы также называем их структурные скобки в отличие от угловых вычислительных скобок. Структурные скобки следует объединять в пары согласно общепринятым простым правилам. Будем называть произвольную последовательность символов, включающую и правильно расставленныe скобки, объектным выражением. Более точно, объектное выражение - это последовательность конечного числа термов, где каждый терм является либо одним символом, либо выражением, заключенным в скобки. Количество термов в выражении может быть и нулем, так что пустое объектное выражение (буквально ничего не содержащее) является допустимым. Вот некоторые примеры выражений:
A
(A'+'B)'*'(C'-'D)
Begin (Ho-ho-ho '(' ('A joke')) End
()
(()'100'100() (()) ) [[
Примеры последовательностей, не являющихся (объектными) выражениями:
) End A ( B)((C) ( A ')';
ЗАМЕЧАНИЕ: Заключение в кавычки каждого
знака, как в одном из рассматриваемых выше
примеров:
(A'+'B)'*'(C'-'D)
может представлять неудобство. Следует, однако, иметь в виду, что подобное заключение необходимо только в тексте РЕФАЛ-программы, где появление больших выражений такого рода маловероятно. Такое выражение типично для данных. Когда оно набирается либо читается из файла как данные, при использовании специальной функции Input , кавычками окружаются только скобочные символы для того, чтобы отличать их от структурных скобок. Мы могли бы, таким образом, набрать:
(A + B) * (C - D)
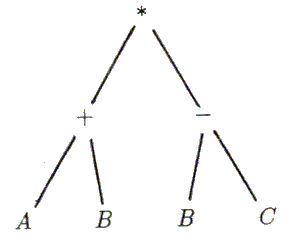
В алгебре мы используем выражения для представления некоторой последовательности операций над числами и переменными; скобки в выражении отмечают порядок выполнения операций. Если выражение, приведенное выше, понимать как алгебраическое, то оно может быть представлено в виде дерева, показанного на Рис. 1.1.

Рис. 1.1 Дерево для алгебраического выражения
Следует подчеркнуть, что концепция выражения в РЕФАЛе является более общей. Мы не предполагаем никакой специальной интерпретации выражений; они могут быть использованы различным образом. РЕФАЛ-выражение просто является структурированным объектом, который сконструирован некоторым способом из символов и структурных скобок. Для каждой структурной скобки в нем имеется в точности одна парная скобка противоположного вида. Вместе они образуют нечто вроде коробки или кармана. Они выделяют такую подсистему во включающей системе, которая является частью целого, но в то же время сохраняет и собственную целостность. Если вы выделяете одну границу в такой подструктуре, то вторая граница определяется единственным образом. Отношение между системой и ее подсистемами является очень важным аспектом окружающего мира. Когда мы создаем символьные модели мира, структурные скобки моделируют такое отношение. Если фортепиано (Piano), скрипка (Violin) и альт (Viola) находятся в квартире Энн (Ann apartment), а виолончель (Cello) и контрабас (Bass) - в квартире Боба (Bob apartment), то эта ситуация может быть промоделирована РЕФАЛ-выражением:
Ann-apt(Piano Violin Viola) Bob-apt(Cello Bass)
РЕФАЛ-выражение может быть представлено деревом так же, как и алгебраическое выражение. Однако, если мы понимаем выражение именно как РЕФАЛ-выражение, без какой-либо интерпретации, дерево должно кое-чем отличаться. На Рис. 1.1 мы располагали операции выше их аргументов. Но если мы не интерпретируем выражение как алгебраическое, то A + B является просто конкатенацией трех символов, и все они должны располагаться на одном и том же уровне. Дерево должно выглядеть, как это показано на Рис. 1.2. Листьями (конечными узлами) дерева являются символы; все другие узлы - это заключенные в скобки подвыражения.
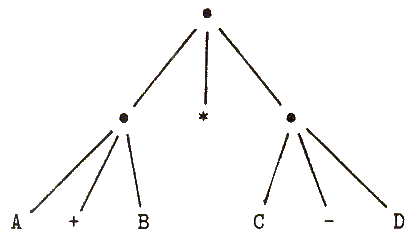
Рис. 1.2 Дерево РЕФАЛ-выражения
Другим способом двумерного графического представления выражений является соединение парных скобок линиями, как бы связывание их веревочками; иерархия подвыражений при этом становится более наглядной (см. Рис. 1.3). Когда РЕФАЛ-выражения представлены в компьютере, адрес пары скобок хранится вместе с каждым членом пары, так что становится возможным совершать скачок от каждой скобки к ее дополняющей за один шаг, как бы пробегая вдоль линий рисунка.
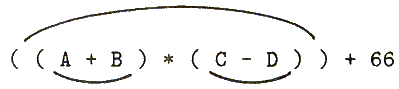
Рис. 1.3 Парные скобки соединены для большей
наглядности.
Упражнение 1.1 Записать строку Joe's Pizza is
"cute" , используя одинарные и двойные
кавычки в качестве ограничителей.
Упражнение 1.2 Записать -236 как целое
число в РЕФАЛе.
Выражения-образцы (или просто образцы) РЕФАЛа отличаются от объектных выражений тем, что они могут включать свободные переменные. Вот некоторые примеры свободных переменных:
e.1 e.Data1 e.data1 s.X s.Free-var t.1 t.25
Свободные переменные состоят из указателя типа, точки и индекса. Индексом переменной является идентификатор либо целое число. Если индекс является однобуквенным идентификатором или одноразрядным числом, точка может быть опущена. Идентификатор, используемый как индекс после точки, может начинаться как со строчной буквы, так и с прописной. Есть три указателя типа. Они обозначаются малыми буквами s , t и e ; соответствующие им переменные называются s-, t- и e-переменными. Различие между ними состоит в множествах их допустимых значений. Значением s-переменной может служит только один символ. Значением t-переменной может быть любой терм (напомним, что терм - это либо символ, либо выражение в структурных скобках). Значением e-переменной может быть любое выражение.
Образец можно рассматривать как множество объектных выражений, которые могут быть получены в результате придания допустимых значений всем переменным. Так, образец A e.1 представляет множество всех объектных выражений, начинающихся с символа A. Всем вхождениям одной и той же переменной следует придавать одно и то же значение. Образец s.1 e.2 s.1 можно рассматривать как множество всех объектных выражений, которые начинаются и заканчиваются одним и тем же символом и состоят по крайней мере из двух символов.
Но выражения-образцы выполняют также еще одну функцию: они описывают декомпозицию объектных выражений, в ходе которой переменные образца отождествляются с некоторыми частями объектного выражения, то есть принимают некоторые значения. С этой точки зрения, A e.1 является процедурой, которая проверяет, что первым символом данного объектного выражения является A , и присваивает остальную его часть переменной e.1 в качестве значения. Эта процедура известна как сопоставление с образцом.
Для заданных объектного выражения E и образца P будем обозначать операцию сопоставления E с P через E : P , где двоеточие - еще один специальный знак РЕФАЛа, знак сопоставления. Будем говорить также, что E распознается как (частный случай) P . В паре E : P назовем E аргументом , а P - образцом операции сопоставления.
Если существует подстановка S для переменных в P такая, что применение S к P приводит к E , тогда будем говорить, что сопоставление, или распознавание, является успешным. Переменные в P принимают значения, предписываемые подстановкой S . В противном случае сопоставление считаем неудавшимся. Если имеется несколько способов присваивания значений свободным переменным в образце, при которых сопоставление может быть успешно, то тогда выбирается такой способ, при котором самая левая e-переменная принимает наиболее короткое значение. Если это не приводит к однозначности, подобный выбор делается для следующей (самой левой) e-переменной, и т.д. Иными словами, при выполнении распознавания аргумент E обозревается слева направо и выбирается первое успешное сопоставление E с P .
Приведем несколько примеров. Сопоставление
A B C : A e.1
считается успешным , если e.1 принимает значение B C . Сопоставление
('ABC') '++' : s.X e.1
терпит неудачу, поскольку левая скобка не символ, так что она не может быть сопоставлена с s.X. С другой стороны, ее нельзя игнорировать. Однако,
('ABC') '++' : (s.X e.1) e.Out
становится успешным, когда s.X присваивается 'A' , e.1 присваивается 'BC' , а e.Out присваивается'++' .
Распознавание '++' как s.1 e.2 s.1 является успешным -- при s.1, принимающем значение '+', и при присвоении e.2 пустого выражения. Но сопоставление
'+' : s.1 e.2 s.1
терпит неудачу.
Следующее сопоставление:
A B '+' C '+' D E F : e.1 '+' e.2
является примером ситуации, когда имеется более чем один способ придания значений для сопоставления. Согласно приведенному выше определению, символ '+' в образце будет идентифицироваться с первым символом '+' в аргументе (сопоставление слева-направо). Таким образом, e.1 примет значение A B, а e.2 - станет цепочкой C '+' D E F.
В следующем примере:
A B '-' (C '+' D E F) : e.1 '+' e.2
сопоставление потерпит неудачу, так как
единственный символ '+' в аргументе
находится внутри скобок. При сопоставлении его с '+'
в образце мы должны были бы присвоить e.1
и e.2 такие значения, которые
несбалансированы по скобкам, а это невозможно.
Структурные скобки в РЕФАЛе - вещь весьма
серьезная. Части выражений, которые сами не
являются выражениями, не могут обрабатываться
самостоятельно ни в каком контексте.
Упражнение 1.3 Запишите образцы, которые могут
быть заданы следующими словесными описаниями: (a)
выражение, оканчивающееся двумя одинаковыми
символами; (b) выражение, которое содержит по
крайней мере два одинаковых терма на верхнем
уровне структуры; (c) непустое выражение.
Упражнение 1.4 Определите результаты
следующих сопоставлений:
(a) 'abbab' : e.1 t.X t.X e.2 (b) 'ab(b)ab' : e.1 t.X t.X e.2 (c) A(B) C D (A (B)) : e.6 e.4(e.6) (d) '16 0' : 16 e.Z
РЕФАЛ-программа есть перечень функциональных определений. Она может также содержать внешние ссылки (которые будут обсуждаться в Главе 2) и комментирующие строки. Комментирующая строка начинается с символа звездочки * , и не влияет на выполнение программы. Комментирующие строки могут вставляться как внутрь функциональных определений, так и между ними. Порядок функциональных определений в программе не имеет значения.
Функциональное определение имеет одну из следующих форм:
имя-функции { блок }
$ENTRY имя-функции { блок }
Значимость префикса $ENTRY будет рассмотрена в Главе 2 наряду с применением внешних ссылок.
Имя функции является идентификатором. Блок есть перечень предложений, разделяемых точками с запятой; последнее предложение также может заканчиваться точкой с запятой. Порядок предложений в функциональном определении является существенным.
Предложение имеет вид:
левая-часть = правая-часть
где левая часть является выражением-образцом, а
правая часть является общим выражением.
Напомним, что объектное выражение может включать
только символы и структурные скобки, а
выражение-образец может, кроме этого, включать и
свободные переменные. Общее же выражение, в
дополнение к составляющим выражения-образца,
может включать еще вычислительные скобки
< и >. Они входят в него как части вызовов
функций:
<имя-функции аргумент>
где имя-функции является либо
индентификатором, либо одним из четырех знаков
арифметических операций (+ , - , *
, и / ); а аргумент является
общим РЕФАЛ-выражением. Таким образом,
вычислительные скобки могут быть вложенными.
Заметим, что имя функции должно следовать
непосредственно за открывающей вычислительной
скобкой, оно не допускает включения пробелов или
конца строки.
Имеются следующие важные ограничения на правую часть предложения: правая часть может включать только такие свободные переменные, которые входят также и в левую часть (см. следующий раздел). Имеется также техническое ограничение: индексы переменных должны быть уникальными, т.е. можно использовать e.X и s.1 любое число раз, но если уже используется e.X , то запрещено использовать s.X или t.X в этом же предложении; использование s.1 исключает применение e- и t-переменных с индексом 1 .
Наряду с комментирующими строками, предложения могут включать длинные комментарии, которые начинаются комбинацией /* и заканчиваются комбинацией */. Они могут появляться всюду при условии, что ими не нарушаются лексические элементы (идентификаторы, числа, строки, переменные) и левая вычислительная скобка не отрывается от следующего за ней имени функции.
РЕФАЛ-машиной называется абстрактное устройство, которое выполняет РЕФАЛ-программы. Она имеет два потенциально бесконечных хранилища информации: поле программы и поле зрения. Поле программы содержит РЕФАЛ-программу, которая загружается в машину перед запуском и не изменяется в ходе выполнения. Поле зрения хранит выражение без свободных переменных; такие выражения называются определенными. Поле зрения (т.е. выражение в этом поле) изменяется в ходе работы машины.
Работа РЕФАЛ-машины осуществляется в пошаговом режиме. Каждый шаг выполняется следующим образом. Если выражение в поле зрения не включает вычислительных скобок (мы будем называть такие выражения пассивными), РЕФАЛ-машина приходит к нормальному останову. В противном случае она выбирает в поле зрения одно из подвыражений вида <F E> , где F является функциональным символом, а E - выражением, для того чтобы трансформировать его, используя определение F из программы. Это подвыражение называется первичным активным подвыражением. Оно определяется как первое (слева) подвыражение <F E >, такое, что E пассивно, т.е. не содержит вычислительных скобок.
Первичное подвыражение <F E > трансформируется следующим образом. РЕФАЛ-машина сравнивает E с последовательными предложениями из определения F, начиная с первого, осуществляя поиск первого применимого предложения.
Предложение применимо, если E может быть распознано как его левая часть L, т.е. сопоставление E : L является успешным. После нахождения первого применимого предложения РЕФАЛ-машина копирует его правую часть R и применяет к ней подстановку, полученную при сопоставлении E : L . Таким образом, свободные переменные в R замещаются значениями, которые они должны принять для успешного сопоставления. Затем определенное выражение, сформированное при этом, замещает первичное активное подвыражение < F E > в поле зрения. Этим завершается текущий шаг и машина переходит к выполнению следующего шага. Если же применимых предложений в определении F не имеется, РЕФАЛ-машина приходит к аварийному останову 'Отождествление невозможно'.
Для того, чтобы вычислить значение некоторой функции F с аргументом E (который должен быть объектным выражением), < F E > помещается в поле зрения РЕФАЛ-машины и машина запускается. Если после конечного числа шагов РЕФАЛ-машина приходит к нормальному останову, то содержимое поля зрения (также объектное выражение) является значением функции. Если же машина зацикливается или приходит к аварийному останову, значение функции считается неопределенным.
Порядок вычисления вложенных вызовов функций, используемый в РЕФАЛ-машине, называется аппликативным или порядком типа изнутри-наружу. Перед запуском вычисления любого вызова функции должны быть завершены все вычисления вызовов функций в аргументе.
Кроме функций, определяемых в РЕФАЛе посредством предложений, существует несколько функций, которые не должны (а во многих случаях и не могут) определяться в РЕФАЛе, но все-таки могут применяться, поскольку они встроены в систему. К этой категории, в числе прочих, относятся функции ввода-вывода и функции выполнения арифметических операций. Реализация РЕФАЛ-машины на компьютере отличается от абстрактной РЕФАЛ-машины тем, что перед просмотром определения функции в поле программы система проверяет, входит ли имя функции в список имеющихся встроенных функций. Если оно обнаружено в списке, активизируется соответствующая подпрограмма, которая выполняет требуемые операции и замещает вызов функции в поле зрения на его вычисленное значение.
1.6. ДАЛЬНЕЙШИЕ ПРИМЕРЫ ФУНКЦИЙ
Допустим, желательно иметь функцию, которая обрабатывает символьные строки и конвертирует каждый знак '+' в '-' . Сперва определим алгоритм словесно:
Теперь выразим это на РЕФАЛе. Пусть именем функции служит Chpm :
* Chpm, Change Plus to Minus
Chpm {
*1.Symbol '+' encountered.Replace by '-':
'+' e.1 = '-' <Chpm e.1>;
*2.Any symbol distinct from '+':
s.2 e.1 = s.2 <Chpm e.1>;
*3.Empty string:
= ;
}
Далее приведена последовательность вычислений для случая, когда аргументом Chpm является 'ab+c-+d' :
<Chpm 'ab+c-+d'> 'a'<Chpm 'b+c-+d'> 'ab'<Chpm '+c-+d'> 'ab-'<Chpm 'c-+d'> 'ab-c'<Chpm '-+d'> 'ab-c-'<Chpm '+d'> 'ab-c--'<Chpm 'd'> 'ab-c--d'<Chpm > 'ab-c--d';
Имеется лучшее решение проблемы. За один шаг РЕФАЛ-машины можно найти первый символ '+' и заменить его на '-' . Если в строке нет ни одного символа '+', она трансформируется в самое себя:
Chpm {
e.1 '+' e.2 = e.1 '-' <Chpm e.2>;
e.1 = e.1; }
При том же аргументе, что и выше, вычисление производится всего за три шага:
<Chpm 'ab+c-+d'> 'ab-'<Chpm 'c-+d'> 'ab-c--'<Chpm 'd'> 'ab-c--d'
Определим в РЕФАЛе функцию факториал для целых неотрицательных чисел. Арифметические функции в РЕФАЛе (см. Главу 2 и Раздел справочника C) имеют имена Add , Sub , Mul , Div . Они могут быть также представлены символами + , - , * и / соответственно.
Fact { 0 = 1;
s.N = <* s.N <Fact <- s.N 1>>>; }
Приведем вычисление <Fact 3> :
<Fact 3> <* 3 <Fact <- 3 1>>> <* 3 <Fact 2>> <* 3 <* 2 <Fact <- 2 1>>>> <* 3 <* 2 <Fact 1>>> <* 3 <* 2 <* 1 <Fact <- 1 1>>>>> <* 3 <* 2 <* 1 <Fact 0>>>> <* 3 <* 2 <* 1 1>>> <* 3 <* 2 1>> <* 3 2> 6
Иногда функции определяются с помощью таблицы. Предположим, мы хотим транслировать итальянские слова в английские. Мы, разумеется, должны различать определение таблицы и определение функции, которая осуществляет перевод с использованием таблицы. Пусть первая именуется Table -- это функция, не имеющая переменных, которая возвращает таблицу в качестве значения. Пусть вторая называется Italian , это функция одной переменной для перевода итальянских слов. Сразу же можно заметить, что функция, которая действительно использует таблицу, должна иметь ее в качестве одного из своих аргументов. Поэтому введем функцию Trans от двух аргументов, которую будем вызывать в формате:
<Trans (e.Word) e.Table>
Скобки отделяют первый аргумент - слово, которое
нужно перевести, - от второго аргумента - таблицы,
которая при этом используется. Теперь можно
определить Ital-Engl через вызов Trans
:
* Translate an Italian word into English
Ital-Engl { e.W = <Trans (e.W) <Table>>; }
Формат таблицы должен быть таким, чтобы необходимое слово могло быть найдено за счет применения простого и эффективного образца . Таблица для пяти итальянских слов может иметь вид:
Table { = (('cane') 'dog')
(('gatto') 'cat')
(('cavallo') 'horse')
(('rana') 'frog')
(('porco') 'pig')
}
При таблице этого формата определение функции Trans имеет вид:
* Translate a word by table
Trans {
(e.Word) e.1 ((e.Word) e.Trans) e.2 = e.Trans;
(e.Word) e.1 = '***'; }
Второе предложение говорит, что если слово не
найдено в таблице, то в перевод подставляются три
звездочки.
Упражнение 1.5 В рекурсивной арифметике
натуральные числа представляются как 0,0',0'', и т.д.
Операция сложения определяется соотношениями:
x + 0 = x x + y' = (x + y)'
Написать наиболее близкий к этому вариант на
РЕФАЛе , используя '0' в качестве 0
и 's' вместо штрих-символа '.
Упражнение 1.6 Определить функцию <Addb
(e.1)(e.2)> , которая складывает двоичные числа e.1
и e.2 .