Глава 11. От Евклида до Декарта
11.1. Число и величина
Во времена Пифагора и ранних пифагорейцев руководящую высоту в греческой математике занимало понятие числа. Пифагорейцы считали: Бог положил числа в основу мирового порядка. Бог — это единство, а мир — множественность. Божественная гармония в устройстве Космоса проявляется в виде числовых отношений. Немалую роль в этом убеждении сыграло открытие пифагорейцами того факта, что сочетания звуков, приятные для слуха (гармонические), создаются в том случае, когда струна укорачивается в отношениях, образуемых минимальными целыми числами: 1:2 (октава), 2:3 (квинта), 3:4 (кварта) и т. д. Числовая мистика пифагорейцев отражала их веру в то, что, в конечном счете, все закономерности природных явлений вытекают из свойств целых чисел.
Мы видим здесь проявление человеческой склонности к переоценке только что сделанных открытий. Физики конца XIX в. полагали подобно пифагорейцам, что они имеют универсальный ключ ко всем явлениям природы и что при надлежащем усердии с его помощью можно раскрыть секрет любого явления. Этот ключ — представление о пространстве, заполненном частицами и полями, которые подчиняются уравнениям Ньютона и Максвелла. Однако с открытием радиоактивности и дифракции электронов высокомерие физиков разлетелось в пух и прах.
В случае с пифагорейцами аналогичную роль сыграло открытие существования несоизмеримых отрезков, т. е. таких отрезков, что отношение их длин не выражается никаким отношением целых чисел (рациональным числом). Не соизмеримы, например, сторона квадрата и его диагональ. Это утверждение легко доказать, опираясь на теорему Пифагора. В самом деле, допустим противное, т. е. что диагональ квадрата находится в некотором отношении m:n к его стороне. Если числа m и n имеют общие множители, их можно сократить, поэтому будем считать, что общих множителей у m и п нет. Значит, при измерении длины некоторым единичным отрезком длина стороны есть n, а диагонали m. Из теоремы Пифагора следует, что должно иметь место равенство m2 = 2n2. Следовательно, m2 должно делиться на 2, а, следовательно, 2 должно быть в числе делителей m, т. е. m = 2m1. Делая эту подстановку, получаем 4m12 = 2n2, т. e. 2m12 = n2. Значит, n также должно делиться на 2, что противоречит предположению об отсутствии у m и n общих множителей. На это доказательство часто ссылается Аристотель. Полагают, что оно было обнаружено еще пифагорейцами.
Если существуют величины, которые при заданном масштабе не выражаются числами, то число не может больше считаться основой основ, оно низвергается со своего пьедестала. Математикам приходится теперь пользоваться более общим понятием геометрической величины, и изучать отношения между величинами, которые иногда (скорее, в виде исключения, чем правила) могут выражаться отношением целых чисел. Такой подход лежит в основе всей греческой математики, начиная с классического периода. Соотношения, которые мы знаем как алгебраические равенства, были известны грекам в геометрической формулировке как отношения между длинами, площадями, объемами построенных определенным образом фигур.
11.2. Геометрическая алгебра
На рис. 11.1 показана хорошо известная геометрическая трактовка соотношения
(a + b)2 = a2 + 2ab + b2.
Столь же тривиальное с алгебраической точки зрения равенство
(a + b)(a - b) = a2 - b2
требует уже более сложного геометрического рассмотрения. Ему соответствует следующая теорема во второй книге «Начал» Евклида (рис. 11.2):
«Если прямая линия разделена на равные и неравные части, то прямоугольник, содержащийся между неравными частями1 всей прямой, вместе с квадратом отрезка между точками деления равен квадрату на половине прямой».
Доказывается теорема следующим образом.
Прямоугольник ABFE равен прямоугольнику BDHF. Прямоугольник BCGF равен прямоугольнику GHKJ. Если к этим двум прямоугольникам (образующим вместе прямоугольник ACGE, «содержащийся между неравными частями всей прямой») добавить квадрат FGJI, то получится как раз квадрат BDKI, построенный «на половине прямой». Итак, мы имеем равенство
(a + b)(a - b) + b2 = a2,
эквивалентное приведенному выше, но не содержащее трудно интерпретируемого вычитания площадей.
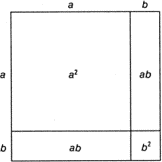
Рис. 11.1. Геометрическая трактовка тождества (a + b)2 = a2 + 2ab + b2
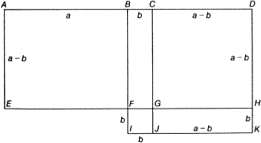
Рис. 11.2. Геометрическая трактовка тождества (a + b)(a - b) = a2 - b2
Ясно, что если даже эти простейшие алгебраические соотношения требуют в геометрической трактовке определенных усилий для понимания формулировки теоремы и изобретательности для ее доказательства, то далеко по этому пути продвинуться невозможно. Во всем, что касается собственно геометрии, греки проявили себя как искуснейшие мастера. Но та линия развития математики, которая началась с алгебры, а затем породила анализ бесконечно малых и современные аксиоматические теории, т. е. линия, связанная с использованием не языка фигур, а языка символов, оказалась им совершенно недоступной. Греческая математика осталась ограниченной, сдавленной узкими рамками понятий, имеющих наглядный геометрический смысл.
11.3. Архимед и Аполлоний
В Александрийскую эпоху (330–200 до н. э.) живут два великих ученых, в работах которых греческая математика достигает своей высшей точки, — Архимед (287–212 до н. э.) и Аполлоний (265?–170? до н. э.). Архимед в своих геометрических трудах уже далеко выходит за пределы фигур, образованных прямыми и окружностями. Он развивает теорию конических сечений, исследует спирали. Главная заслуга Архимеда в геометрии — многочисленные теоремы о площадях, объемах и центрах тяжести фигур и тел, образованных не только прямыми линиями и не только плоскими поверхностями. Он использует «метод исчерпывания». Чтобы проиллюстрировать круг задач, решаемых Архимедом, перечислим задачи, вошедшие в его сочинение «Метод», цель которого, как это видно из заглавия, не полная сводка результатов, а освещение метода работы. «Метод» содержит решение следующих 13 задач: площадь параболического сегмента, объем шара, объем сфероида (эллипсоида вращения), объем сегмента параболоида вращения, центр тяжести сегмента параболоида вращения, центр тяжести полушария, объем сегмента шара, объем сегмента сфероида, центр тяжести сегмента шара, центр тяжести сегмента сфероида, центр тяжести сегмента гиперболоида вращения, объем сегмента цилиндра, объем пересечения двух цилиндров (последняя задача — без доказательства).
Не меньшее значение, чем работы по геометрии, имели исследования Архимеда в области механики. Он открыл свой знаменитый «закон Архимеда», занимался законами равновесия тел. Он был необыкновенно искусен в изготовлении различных механических устройств и приспособлений. Благодаря машинам, сделанным под руководством Архимеда, жители его родного города Сиракузы отразили первый штурм города римлянами. Механические соображения часто использовались Архимедом в качестве подспорья при выводе геометрических теорем. Однако было бы ошибкой полагать, что Архимед хотя бы в чем-то отклонялся от традиционного греческого образа мышления. Он считал задачу решенной только тогда, когда находил безупречное с логической точки зрения геометрическое доказательство. Свои механические изобретения он рассматривал как забаву или же, как житейские занятия, не имеющие никакого научного значения. Плутарх пишет:
Хотя эти изобретения прославили его сверхчеловеческую мудрость, тем не менее он ничего не писал по таким вопросам, ибо полагал, что сооружение всякого рода машин и вообще всех приспособлений для практического употребления — дело низкое и неблагородное; сам же он стремился лишь к тому, что по красоте своей и совершенству находится далеко от царства необходимости.
Из всех своих достижений сам Архимед больше всего гордился доказательством того, что объем шара, вписанного в цилиндр, составляет две трети объема цилиндра. Он завешал изобразить на своей могильной плите цилиндр с вписанным в него шаром. Римский полководец Марцелл, солдат которого убил Архимеда после взятия Сиракуз, (как утверждают, вопреки распоряжению Марцелла), разрешил родственникам Архимеда выполнить завещание покойного.
Аполлоний прославился, главным образом, своей работой по теории конических сечений. Фактически эта работа — последовательное алгебраическое исследование кривых второго порядка, выраженное на геометрическом языке. В наше время все результаты, полученные Аполлонием, может легко проверить любой студент, используя методы аналитической геометрии. Но, чтобы сделать то же в рамках чисто геометрического подхода, Аполлонию потребовалось проявить чудеса математической интуиции и изобретательности.
11.4. Упадок греческой математики
Б. Ван дер Варден пишет2:
После Аполлония греческая геометрия сразу кончается. Правда, были еще эпигоны, вроде Диокла и Зенодора, которые время от времени решали некоторые задачи, оставшиеся им от Архимеда и Аполлония, словно крохи от пира великих. Писались еще, правда, произведения типа сборников вроде сочинения Паппа Александрийского (300 г.); математика еще применялась для практических или астрономических задач, причем разрабатывалась плоская и сферическая тригонометрия. Но, кроме тригонометрии, ничего значительного, ничего нового уже не появлялось. Геометрия конических сечений дожила до Декарта в той форме, какую придал ей Аполлоний; произведения Аполлония читались очень мало, а частью были также утрачены. «Метод» Архимеда также был потерян из вида, и проблема интегрирования оставалась без движения, пока за нее не взялись снова в XVII в. ...
Упадок греческой математики частично был вызван причинами внешнего порядка — политическими бурями, охватившими Средиземноморскую цивилизацию. Однако решающее значение имели все же внутренние причины. В астрономии, замечает Ван дер Варден, развитие шло все время по восходящей линии; тут бывали короткие и длинные остановки, но после их окончания работа возобновлялась с того места, где она остановилась. В геометрии же имел место явный регресс. Причина кроется, конечно, в отсутствии алгебраического языка. У Ван дер Вардена мы читаем:
Уравнения первой и второй степени можно было хорошо передать на языке геометрической алгебры; в крайнем случае, это было возможно для уравнений третьей степени. Но пойти дальше можно было, только пользуясь громоздкими и утомительными средствами пропорций.
Гиппократ, например, приводил кубические уравнения x3 = V к пропорции
a : х = х : у = у : b,
а Архимед писал уравнение третьей степени
х2(a - х) = bс2
в виде пропорции
(a - x) : b = c2 : x2.
Этим путем еще можно добраться до уравнений четвертой степени; примеры этого, пожалуй, можно найти и у Аполлония. Однако дальше пойти нельзя; больше того, чтобы получать результаты этим в высшей степени сложным методом, нужно было еще обладать математическим гением и быть весьма искушенным по части преобразования пропорций при помощи геометрических фигур. Нашими алгебраическими обозначениями может пользоваться каждый инженер или естествоиспытатель, а греческой теорией пропорций и геометрической алгеброй —только очень одаренный математик.
К этому присоединяется еще другое обстоятельство, а именно трудность письменной передачи.
Чтение доказательств у Аполлония требует долгого и напряженного размышления. Вместо удобной алгебраической формулы стоит длинная фраза, где каждый отрезок обозначается двумя буквами, которые всякий раз еще нужно отыскивать на чертеже. Чтобы понять ход мыслей, приходится заменять эти фразы современными сжатыми формулами...
При устном объяснении на отрезки можно указывать пальцем, можно делать ударение на особенно важных местах и, кроме того, можно рассказать, каким образом получилось доказательство. Все это отпадает в письменной формулировке строго классического стиля: доказательства закончены, логически обоснованы, но они ничего не подсказывают. Не можешь ничего возразить, чувствуешь, что попался в логическую мышеловку, но не видишь, какая основная линия рассуждений за этим скрывается.
Таким образом, пока еще традиция не прерывалась, пока каждое поколение могло передавать свою методику следующему, все шло хорошо и наука процветала. Но как только по ряду причин внешнего характера устная передача прерывалась, и оставались только одни книги, понимать труды великих предшественников становилось крайне трудно, а выйти за их пределы и двинуться вперед — почти невозможно.
Почему же греки, несмотря на их высокую математическую культуру и обилие одаренных математиков, так и не смогли создать алгебраического языка? Обычный ответ на этот вопрос таков, что этому помешала именно их высокая математическая культура, конкретнее — высокий уровень требований к логической строгости теории, ибо иррациональные числа, которыми, как правило, выражаются значения геометрических величин, греки не могли рассматривать как числа; если отрезки были несоизмеримы, то считалось, что числового отношения для них просто не существует. Это объяснение, хотя оно и верно в общих чертах, следует вместе с тем признать неточным и поверхностным. Стремление к логической строгости не может быть само по себе отрицательным фактором в развитии математики. Если оно выступает в качестве отрицательного фактора, то, очевидно, лишь в комбинации с какими-то другими факторами и вряд ли следует решающую роль в этой комбинации приписывать именно стремлению к строгости. Совершенная логическая строгость в окончательных формулировках и доказательствах не мешала Архимеду пользоваться нестрогими наводящими соображениями. Почему же она помешала созданию алгебраического языка? Здесь дело, конечно, не просто в высоком стандарте логической строгости, а во всем строе мышления, в философии математики. Декарт, создав современный алгебраический язык, вышел за рамки греческого канона, но это вовсе не значит, что он погрешил против законов логики или пренебрегал доказательствами. И иррациональные числа он мыслил как «точные», а вовсе не как замененные на свои приближенные значения. Некоторые неполадки с логикой начались уже после Декарта, в эпоху бурного развития анализа бесконечно малых. Тогда математики были так увлечены потоком открытий, что им просто было не до логических тонкостей. В XIX в. появилось время подумать, и под анализ была подведена более прочная логическая основа.
Причины ограниченности греческой математики мы уясним себе после того, как разберем сущность переворота в математике, произведенного Декартом.
11.5. Арифметическая алгебра
Успехи геометрии оттеснили на задний план искусство решения уравнений. Однако оно продолжало развиваться и породило арифметическую алгебру. Возникновение алгебры из арифметики — это типичный метасистемный переход. Когда ставится задача о решении уравнения — независимо от того, формулируется ли она на обычном разговорном языке или на специализированном, — это еще задача арифметическая. И когда указывается общий метод решения — на примерах, как это делается в начальной школе, или даже в виде формулы, мы все еще не выходим за пределы арифметики. Алгебра начинается тогда, когда сами уравнения становятся объектом деятельности, когда изучаются свойства уравнений и правила их преобразования. Наверно, каждый, кто помнит, как он познакомился с алгеброй в школе (если только это было на уровне понимания, а не зазубривания), помнит и то радостное чувство изумления, которое испытываешь, когда оказывается, что разнотипные арифметические задачи, приемы решения которых представлялись друг с другом совершенно не связанными, решаются путем однотипных преобразований уравнений по нескольким простым и понятным правилам. Все ранее известные методы вписываются в стройную систему, открываются новые методы, вводятся в рассмотрение новые уравнения и целые классы уравнений (закон разрастания предпоследнего уровня), появляются новые понятия, не имеющие решительно никакого смысла в рамках собственно арифметики: отрицательные, иррациональные и мнимые числа.
Принципиальной необходимости создания специализированного языка для развития алгебры нет. Однако на деле только созданием специализированного языка завершается метасистемный переход в головах людей. Специализированный язык дает возможность убедиться, что мы имеем дело с некоей новой реальностью — в данном случае с уравнениями, которые можно рассматривать как объект выкладок, подобно объектам предыдущего уровня — числам. Людям свойственно не замечать воздуха, которым они дышат, и языка, которым все время пользуются. Созданный же вновь специализированный язык выпадает из сферы естественного языка и представляется частью неязыковой действительности. Это способствует метасистемному переходу. И, конечно, огромную роль играют практические удобства использования специализированного языка: обозримость выражений, уменьшение затрат на переписывание и т. п.
Арабский ученый Мухаммед ибн Муса ал-Хорезми (780–850) написал несколько сочинений по математике, которые в XII в. были переведены на латынь и на протяжении четырех столетий служили в Европе важнейшими учебными пособиями. Одно из них — «Арифметика» — донесло до европейцев десятичную систему счисления и правила (алгоритмы — от имени ал-Хорезми) выполнения четырех действий арифметики над числами, записанными по этой системе. Другое сочинение называлось «Книга об ал-джебр и ал-мукабала». Оно имело целью обучить искусству решения уравнений, которое необходимо, по словам автора, «в случаях наследования, раздела имущества, торговли и во всех деловых взаимоотношениях, а также при измерении земель, проведении каналов, геометрических вычислений и в других случаях...» «Ал-джебр» и «ал-мукабала» – два приема, которые ал-Хорезми использует для решения уравнений. Эти приемы он придумал не сам, они описываются и используются уже в «Арифметике» позднегреческого математика Диофанта (III в.), прославившегося своими методами решения целочисленных (диофантовых) уравнений. В той же «Арифметике» Диофанта встречаются и зачатки буквенной символики. Поэтому если считать кого-то родоначальником арифметической алгебры, то, очевидно, это будет Диофант. Однако в Европе об алгебраических приемах узнали впервые от ал-Хорезми, а труды Диофанта стали известны гораздо позже. Никакой специальной алгебраической символики, даже в зачаточном состоянии, у ал-Хорезми нет. Уравнения фигурируют в виде записи на естественном языке. Но мы для краткости опишем эти приемы и приведем пример, пользуясь современной символикой.
Ал-джебр — это перенесение вычитаемых членов из одной части уравнения в другую; ал-мукабала — вычитание из обеих частей уравнения одинакового члена. Эти приемы ал-Хорезми рассматривает как различные, ибо понятие об отрицательном числе у него отсутствует.
Возьмем для примера уравнение
7x - 11 = 5x - 3.
Применяя прием ал-джебр два раза — для вычитаемого 11 и для вычитаемого 3, получаем
7x + 3 = 5x + 11.
Теперь применим два раза прием ал-мукабала — для члена 3 и для члена 5х. Получаем
2x = 8.
Отсюда х = 4.
Итак, хотя ал-Хорезми не использует специального алгебраического языка, его книга содержит первые наметки алгебраического подхода. Европейцы по достоинству оценили этот подход и дали ему дальнейшее развитие. Само слово «алгебра» происходит от названия первого из приемов ал-Хорезми.
11.6. Италия, XVI век
В первой половине XVI в. благодаря усилиям итальянских математиков в алгебре происходят крупные сдвиги, сопровождаемые весьма драматическими событиями. Профессор Болонского университета Сципион Даль Ферро (1465–1526) находит общее решение уравнения третьей степени
х3 + рх = q
при положительных р и q, но держит его в секрете, ибо оно представляет большую ценность на соревнованиях по решению задач, которые тогда широко практиковались в Италии. Перед смертью он открывает секрет своему ученику Фиоре. В 1535 г. Фиоре вызывает на соревнование талантливейшего математика Никколо Тарталью (1499–1557), который, зная, что Фиоре обладает способом решения кубического уравнения, прилагает максимум усилий и сам находит решение! Тарталья побеждает на соревновании, но также держит свое открытие в секрете. Наконец, на сцене появляется Джероламо Кардано (1501–1576). Он тщетно пытается найти алгоритм решения кубического уравнения и в 1539 г. обращается к Тарталье с просьбой поведать ему тайну. Взяв с Кардано «священную клятву» молчания, Тарталья частично и в не слишком вразумительной форме приоткрывает для него завесу. Кардано не удовлетворяется и прилагает усилия, чтобы ознакомиться с рукописью покойного Даль Ферро. Это ему удается, и в 1545 г. он публикует книгу, в которой сообщает алгоритм, сводящий решение кубического уравнения к радикалам («формула Кардано»). В этой же книге содержится еще одно открытие, сделанное учеником Кардано Луиджи (Лудовико) Феррари (1522–1565), а именно решение в радикалах уравнения четвертой степени. Тарталья обвиняет Кардано в нарушении клятвы, завязывается острая и продолжительная полемика. При таких обстоятельствах заявляет о своих первых существенных достижениях математика Нового времени.
Использование инструмента подсказывает пути к его усовершенствованию. Стремясь к единообразному решению уравнений, математики обнаружили, что для достижения этой цели чрезвычайно полезно внести некоторые новые объекты и обращаться с ними так, как если бы это были числа. Их и называют числами, хотя понимают, что они отличаются от «настоящих» чисел; это проявляется в том, что им придают такие эпитеты, как «ложные», «фиктивные», «непостижимые», «мнимые». Чему они соответствуют в действительности, остается не совсем ясным или совсем неясным. Законно ли их использование, тоже остается спорным. Тем не менее, их используют все шире, ибо с их помощью получаются конечные результаты, которые содержат лишь «настоящие» числа и которые нельзя получить иначе. Человек, последовательно придерживающийся учения Платона, не мог бы использовать «ненастоящие» числа. Однако индийские, арабские и итальянские математики отнюдь не были последовательными платониками; здоровое любопытство и прагматические соображения перевешивали для них теоретическую недозволенность. Правда, при этом они все-таки делали оговорки и как бы извинялись за свое «некорректное» поведение.
Все «ненастоящие» числа — продукт обратного хода арифметической модели, они формально являются решениями таких уравнений, которые не имеют решения в области «настоящих» чисел. В первую очередь надо назвать отрицательные числа. Мы находим их уже в довольно развитом виде у индийского математика Бхаскары (XII в.), который совершает над ними все четыре действия арифметики. Интерпретация отрицательного числа как долга (в противоположность имуществу) была известна индусам еще в XII в. Бхаскара, формулируя правила действий над отрицательными числами, называет их «долг», а положительные — «имущество». Объявить отрицательное число таким же абстрактным понятием, как положительное число, он не решается. «Люди не одобряют отвлеченных отрицательных чисел», — пишет Бхаскара. Примерно так же относятся к отрицательным числам и в Европе XV–XVI вв. При геометрической интерпретации отрицательные корни называют «ложными» в отличие от «истинных» положительных корней. Современная интерпретация отрицательных чисел как точек, лежащих левее точки нуль, появилась только в «Геометрии» Декарта (1637 г.). По традиции Декарт называл отрицательные корни «ложными».
Формальные действия над корнями из чисел, которые не извлекаются в точном виде, восходят к глубокой древности, когда еще не было понятия о несоизмеримости отрезков. В XV–XVI вв. с ними обращаются совсем запросто — помогает здесь, конечно, простая геометрическая интерпретация. Понимание теоретической трудности, вытекающей из несоизмеримости отрезков, проявляется в названии этих чисел: «иррациональные», т. е. не постижимые разумом.
Квадрат любого числа положителен, поэтому квадратного корня из отрицательного числа не существует среди положительных, отрицательных, рациональных или иррациональных. Однако Кардано осмелел настолько, что стал формально оперировать (не без оговорок) с корнями из отрицательных чисел. Так в XVI в. возникли самые невозможные из всех невозможных чисел — «мнимые». Логика использования алгебраического языка неудержимо влекла математиков по неизведанному пути. Он казался незаконным и таинственным, но интуиция подсказывала, что все эти невозможные числа имеют глубокий смысл и новый путь себя оправдает. Так оно и оказалось.
11.7. Буквенная символика
Зачатки алгебраической буквенной символики встречаются впервые, как уже говорилось, у Диофанта. Диофант обозначал неизвестное знаком, напоминающим греческую букву ς или латинскую S. Есть предположение, что это обозначение происходит от последней буквы греческого слова άριθμός — число. Были у него также сокращенные обозначения для квадрата, куба и других степеней неизвестной величины. Знака сложения не было, складываемые величины писались подряд. Знаком вычитания служило нечто вроде перевернутой греческой буквы ψ знаком равенства — первая буква греческого слова ίσος — равный. Все остальное выражалось в словесной форме. Известные величины всегда записывались в конкретной числовой форме, обозначений для известных, но произвольных чисел нет.
«Арифметика» Диофанта стада известна в Европе в 1463 г. С конца XV – начала XVI вв. сначала итальянские, а затем и другие европейские математики начинают пользоваться сокращенными обозначениями. Постепенно эти сокращения перекочевывают из арифметической алгебры в геометрическую — буквами начинают обозначать также неизвестные геометрические величины. В конце XVI в. француз Виет (1540–1603) делает следующий важнейший шаг — вводит буквенные обозначения для известных величин и получает тем самым возможность записывать уравнение в общем виде. Он же вводит термин «коэффициент». По внешнему виду символика Виета еще довольно далека от современной. Например, Виет пишет
|
вместо нашего |
|
К началу XVII в. ситуация в европейской математике была такова. Существовало две алгебры: первая — арифметическая, основанная на символике, созданной самими европейцами, и сделавшая существенный шаг вперед по сравнению с арифметикой древних; вторая — алгебра геометрическая — входила в состав геометрии. Она была почерпнута, как и геометрия в целом, от греков: основы — из «Начал» Евклида, дальнейшее развитие — главным образом из трудов Паппа Александрийского и Аполлония, которые к тому времени были хорошо изучены. Ничего существенно нового в ней сделано не было. Нельзя сказать, что между этими двумя алгебрами совсем не было связи: уравнения степени выше первой могли получить только геометрическую интерпретацию, ибо где еще могли возникнуть квадраты, кубы и высшие степени неизвестного числа, как не при вычислении площадей, объемов или при манипуляциях над отрезками, связанными сложной системой пропорций. Сами названия второй и третьей степени — квадрат и куб — говорят об этом весьма красноречиво. Тем не менее, разрыв между понятиями величины и числа оставался и в полном соответствии с греческим каноном настоящим доказательством считалось только геометрическое. Когда в уравнениях появлялись геометрические объекты — длины, площади, объемы, то они выступали либо как геометрические величины, либо как именованные числа. Геометрические величины мыслились обязательно как нечто пространственное и из-за наличия несоизмеримости не сводимое к числу.
В этой обстановке и сказал свое слово один из величайших мыслителей, когда-либо живших на земле, Ренэ Декарт (1596–1650).
11.8. Что сделал Декарт?
Роль Декарта как философа общепризнанна. Но, говоря о Декарте как о математике, обычно указывают, что он «усовершенствовал алгебраические обозначения и создал аналитическую геометрию». Иногда к этому добавляют, что примерно в то же самое время основные положения аналитической геометрии были выдвинуты независимо от Декарта его соотечественником Пьером Ферма (1601–1665), а что касается алгебраической символики, то ее уже вовсю использовал Виет. Выходит, что в области математики Декарту особенно похвастаться нечем, и, действительно, далеко не все авторы, пишущие об истории математики, отдают ему должное. Между тем Декарт произвел революцию в математике, он создал нечто несравненно большее, чем аналитическая геометрия (понимаемая как теория кривых на плоскости), а именно: новый подход к описанию явлений действительности — современный математический язык.
Иногда говорят, что Декарт «свел геометрию к алгебре», понимая под алгеброй, конечно, алгебру числовую, арифметическую. Это грубая ошибка. Верно, что Декарт преодолел пропасть между величиной и числом, между геометрией и арифметикой, но достиг он этого не сведением одного языка к другому, а созданием нового языка — языка алгебры. По синтаксису новый язык совпадает с арифметической алгеброй, но по семантике — с геометрической. Символы в языке Декарта обозначают не числа и не величины, а отношения величин. В этом — вся суть переворота, произведенного Декартом.
Современный читатель, пожалуй, недоуменно пожмет плечами: какая разница? Неужели этот логический нюанс мог иметь серьезное значение? Оказывается, мог. Именно этот нюанс помешал грекам сделать следующий шаг в своей математике.
Мы настолько привыкли ставить иррациональные числа на одну доску с рациональными, что перестали отдавать себе отчет в том, какое глубокое различие лежит между ними. Мы пишем √2 точно так же, как пишем 4/5, и называем √2 числом, а когда нужно, заменяем на приближенное значение, и мы никак не можем понять, почему древние греки так болезненно реагировали на несоизмеримость отрезков. Но если немного подумать, то нельзя не согласиться с греками, что √2 — это не число. Его можно представить как бесконечный процесс, порождающий последовательные знаки разложения в десятичную дробь. Можно представить его также в виде сечения в области рациональных чисел, т. е. как некое правило, которое делит все рациональные числа на два класса: те, которые меньше √2 и которые больше √2. В данном случае правило весьма простое: рациональное число a относится к первому классу, если a2 < 2 и ко второму — в противном случае. Можно, наконец, представить √2 в виде отношения между двумя отрезками; в данном случае — между диагональю квадрата и его стороной. Эти представления эквивалентны между собой, но никак не эквивалентны представлению о целом или дробном числе.
Значит ли это, что мы совершаем ошибку или нестрогость, обращаясь с корнем из двух как с числом? Отнюдь нет. Цель математики — создание языковых моделей действительности, и хороши все средства, ведущие к этой цели. Почему бы нашему языку наряду со знаками типа 4/5 не содержать и знаки типа √2? «Мой язык — что хочу, то и делаю». Важно только, чтобы мы умели интерпретировать эти знаки и совершать над ними языковые преобразования. Но интерпретировать √2 мы умеем. В практических вычислениях основой интерпретации может служить первое из приведенных выше представлений, в геометрической теории — третье. Умеем мы и производить выкладки с ними.
Теперь осталось только уточнить терминологию. Условимся то, что мы раньше называли числами, называть рациональными числами, новые объекты называть иррациональными числами, а просто числами (действительными числами по современной математической терминологии) называть и те и другие.
Итак, в конечном счете никакой принципиальной разницы между √2 и 4/5 нет и мы оказались мудрее греков. Эту мудрость протаскивали контрабандой все те, кто оперировал со знаком √2 как с числом, признавая вместе с тем, что оно «иррационально». Обосновал и узаконил эту мудрость Декарт.
11.9. Отношение как объект
Тот факт, что греки не создали алгебры, имеет глубокие корни и в философии. У них не было даже арифметической алгебры — это первое и наиболее внешнее, можно даже сказать побочное, следствие их философии. Их мало интересовали арифметические уравнения, ведь уже уравнения второй степени не имеют, вообще говоря, точных числовых решений. А приближенные вычисления и все, что было связано с практическими задачами, их не интересовало. Зато решение могло быть найдено путем геометрического построения! Но, если даже предположить, что греческие математики школы Платона познакомились бы с арифметической буквенной символикой, трудно представить, чтобы они воспроизвели научный подвиг Декарта. Ведь отношение не было для них идеей и не имело, следовательно, реального существования. Кому же придет в голову обозначать буквой то, чего нет? Платоновская идея — это обобщенный образ, форма, свойство: то, что можно представить в воображении как более или менее обобщенный предмет. Все это является первичным и имеет независимое существование, причем существование даже более реальное, чем чувственно воспринимаемые вещи. А что такое отношение отрезков? Попробуйте его представить, и вы сразу увидите, что представляете себе никакое не отношение, а просто два отрезка. Понятие отношения величин отражает процесс измерения одной из них с помощью другой. Но процесс — это не идея в платоновском понимании, это нечто вторичное и не существующее реально: идеи вечны и неизменны и хотя бы уже поэтому не имеют ничего общего с процессами.
Интересно, что понятие отношения величин, отражающее свойства процесса измерения, было в строгой математической форме введено еще Евдоксом и вошло в пятую книгу «Начал» Евклида. Именно это понятие и было использовано Декартом. Однако объектом отношение не было ни у Евдокса, ни у последующих греческих математиков; будучи едва введено, оно немедленно уступило место пропорции, которую легко представить как свойство четырех отрезков, образуемых при пересечении сторон угла двумя параллельными линиями.
Понятие отношения величин — это языковый конструкт, и довольно сложный, а платонизм мешал вводить а математику конструкты, ограничивал ее базисные понятия четко представимыми статическими пространственными образами. В школе Платона даже дроби считались чем-то незаконным с точки зрения настоящей математики. В «Государстве» мы читаем: «Если ты захочешь делить единицу, то ученые математики высмеют тебя и не позволят это сделать; если же ты размениваешь единицу на мелкие деньги, они полагают её обращенной во множество и остерегаются рассматривать единицу не как единое, но состоящее из многих частей». При таком отношении к рациональному числу, что уж говорить об иррациональном!
Кратко подвести итог влиянию платоновского идеализма на греческую математику можно следующим образом. Осознав математические утверждения как объект работы, греки совершили метасистемный переход огромной важности, но они тут же объективизировали базисные элементы математических утверждений, стали рассматривать их как часть неязыковой действительности — «мира идей». Тем самым они закрыли себе путь к дальнейшей эскалации критического мышления — осознанию базисных элементов (понятий) математики как явлений языка и созданию все более и более сложных математических конструктов. Развитие математики в Европе было непрерывным освобождением от оков платонизма.
11.10. Декарт и Ферма
Очень поучительно сравнить математические работы Декарта и Ферма. Как математик Ферма был не менее, а, пожалуй, более одаренным, чем Декарт. Это видно из его замечательных работ по теории чисел. Но он был восхищенным поклонником греков и продолжателем их традиций. Свои открытия по теории чисел Ферма изложил в замечаниях на полях «Арифметики» Диофанта. Его работы по геометрии возникли в результате усилий доказать некоторые положения, на которые Папп ссылался как на принадлежащие Аполлонию, не приводя, однако, доказательства. Размышляя над этими проблемами, Ферма стал систематически использовать представление положения точки на плоскости длинами двух отрезков — абсциссы и ординаты и представление кривой в виде уравнения, связывающего эти отрезки. Идея эта с геометрической точки зрения отнюдь не была новой: она является стержневой не только у Аполлония, но уже у Архимеда и восходит к еще более древним авторам. Архимед описывает конические сечения через их «симптомы», т. е. пропорции, связывающие абсциссы и ординаты точек. Возьмем, например, эллипс с большой осью AB (рис. 11.3). Перпендикуляр PQ, опущенный из некоторой точки эллипса Р на ось AB, называется «ординатой», а отрезки AQ и QB — «абсциссами» этой точки (оба термина — латинские переводы греческих терминов Архимеда). Отношение площади квадрата, построенного на ординате, к площади прямоугольника, построенного на двух абсциссах, одинаково для всех точек Р, лежащих на эллипсе. Это и есть «симптом» эллипса, т. е. по существу уравнение. Его можно записать в виде
y2 : (x1 × x2) = const.
Аналогичные симптомы устанавливаются для гиперболы и параболы. Чем это не система координат?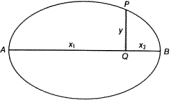
Рис. 11.3. Ордината и абсциссы эллипса
Ферма в отличие от древних формулирует симптомы не в виде словесно описанных пропорций, а в виде уравнений на языке Виета. Это облегчает преобразования; в частности, сразу видно, что вместо двух абсцисс удобнее оставить одну. Но подход остается чисто геометрическим, пространственным.
Ферма изложил свои идеи в трактате «Введение в изучение плоских и телесных мест». Он был опубликован только в 1679 г. уже после смерти автора, но стал известен французским математикам еще в 30-х годах, несколько раньше, чем математические работы Декарта.
Знаменитая «Геометрия» Декарта вышла в свет в 1637 г. Никакого влияния со стороны Ферма Декарт, конечно, не испытал (неизвестно даже, читал ли он трактат Ферма); метод Декарта сложился задолго до выхода «Геометрии», еще в 20-х годах. Тем не менее, собственно геометрические идеи Декарта и Ферма практически тождественны. Но Декарт создал новую алгебру, основанную на понятии отношения геометрических величин. У Виета можно складывать и вычитать только однородные величины и в коэффициенты обязательно включается указание на их геометрическую природу. Например, уравнение, которое мы записали бы в виде
A3 + BA = D,
Виет записывал так:
A cubus +B planum in A aequatur D solido,
т. е. к кубу с ребром A прибавить площадь B, помноженную на A, равно объему D. Виет и Ферма идейно находятся в плену геометрической алгебры греков. Декарт решительно порывает с ней. Отношения, с которыми имеет дело алгебра Декарта, не геометрические пространственные объекты, а умозрительные понятия — «числа». Он не стеснен требованием однородности слагаемых и вообще требованием пространственной интерпретации; возведение в степень он понимает как многократное умножение и указывает число множителей маленькой цифрой выше и правее переменной. Символика Декарта практически совпадает с современной.
11.11. Путь к открытию
Ферма был только математиком. Декарт был прежде всего философом. Его размышления выходили далеко за пределы математики и имели дело с проблемами сущности бытия и познания. Декарт — основоположник философии рационализма, утверждающей неограниченную способность человека познавать мир, исходя из некоторого числа интуитивно ясных истин и продвигаясь, шаг за шагом вперед с помощью определенных правил или методов. Эти два слова — ключевые для всей философии Декарта. «Правила для руководства ума» — так называется его первое философское сочинение, «Рассуждение о методе» — второе. «Рассуждение о методе» было издано в 1637 г. в одном переплете с тремя физико-математическими трактатами: «Диоптрика», «Метеоры» и «Геометрия» и предшествовало им как изложение философских принципов, лежащих в основе следующих частей. Декарт выдвигает в этом сочинении следующие четыре принципа исследования:
- Не признавать истинным ничего, кроме того, что с очевидностью познается мною таковым, т. е. тщательно избегать поспешности и предубеждений и принимать в свои суждения только то, что представляется моему уму так ясно и отчетливо, что ни в коем случае не возбуждает во мне сомнения.
- Разделять каждое из рассматриваемых мною затруднений на столько частей, на сколько возможно и сколько требуется для лучшего их разрешения.
- Мыслить по порядку, начиная с предметов наиболее простых и легко познаваемых, и восходить мало-помалу, как по ступеням, до познания наиболее сложных, допуская существование порядка даже среди тех, которые не следуют естественно друг за другом.
- Составлять повсюду настолько полные перечни и такие общие обзоры, чтобы быть уверенным, что ничего не пропущено.
Руководствуясь этими принципами, Декарт и приходит к своим математическим идеям. Вот как он сам описывает этот путь в «Рассуждении о методе»:
Мне не стоило большого труда отыскание того, с чего следует начинать, так как я уже знал, что начинать надо с самого простого и доступного пониманию; учитывая, что среди всех, кто ранее исследовал истину в науках, только математики смогли найти некоторые доказательства, т. е. представить доводы несомненные и очевидные, я уже не сомневался, что начинать надо именно с тех, которые исследовали они... Но я не имел намерения изучать на этом основании все отдельные науки, обычно именуемые математикой. Видя, что хотя их предметы различны, но все же они сходны между собой в том, что рассматривают не что иное, как различные встречающиеся в предметах отношения, я подумал, что мне следует лучше исследовать эти отношения вообще, мысля их не только в тех предметах, которые облегчали бы мне их познание, и никоим образом не связывая с этими предметами, чтобы тем лучше применить их потом ко всем другим, к которым они подойдут. Затем, приняв во внимание, что для изучения этих отношений мне придется рассматривать каждое из них в отдельности и лишь иногда запоминать или истолковывать их по несколько вместе, я подумал, что для лучшего рассмотрения их в отдельности я должен представить их себе в виде линий, потому что я не находил ничего более простого, что я мог бы представить себе более отчетливо в своем воображении и ощущении. Но для того, чтобы лучше удержать их в памяти или сосредоточить внимание сразу на нескольких, надо выразить их какими-то возможно более краткими знаками. Благодаря такому способу, я мог заимствовать все лучшее в геометрическом анализе и в алгебре и исправить все недостатки одного при помощи другой.
Из этого чрезвычайно интересного свидетельства видно, что Декарт отчетливо осознает семантическую новизну своего языка, основанного на абстрактном понятии отношения и применимого ко всем явлениям действительности. Линии служат лишь для иллюстрации понятия отношения подобно тому, как набор палочек служит для иллюстрации понятия числа. В математических работах то, что обозначается буквами, Декарт и последующие математики называют по традиции величинами, но по смыслу это не пространственные геометрические величины греков, а их отношения. Понятие величины у Декарта так же абстрактно, как понятие числа. Но оно, конечно, никак не сводится к понятию числа в точном смысле слова, т. е. рационального числа. В «Геометрии», поясняя свои обозначения, Декарт указывает, что они подобны (а не тождественны) обозначениям арифметической алгебры.
Подобно тому, как вся арифметика состоит только из четырех–пяти действий, а именно: сложения, вычитания, умножения, деления и извлечения корня... так и в геометрии для нахождения искомых отрезков надо только прибавлять или отнимать другие отрезки; или, имея отрезок, который я для более наглядного сопоставления с числами буду называть единицей и который вообще можно выбирать произвольно и, имея, кроме него, два других отрезка, требуется найти четвертый, который так относится к одному из этих двух, как другой к единице, — это равносильно умножению; или же требуется найти четвертый отрезок, который так относится к одному из двух данных, как единица к другому, — это равносильно делению; или, наконец, требуется найти одно, два или несколько средних пропорциональных между единицей и другим отрезком — это равносильно извлечению корня — квадратного, кубического и т. д. И я нисколько не колеблюсь ввести эти арифметические термины в геометрию, чтобы сделать мое изложение более понятным.
Семантика алгебраического языка Декарта много сложнее семантики арифметического и геометрического языков, опирающихся на наглядные образцы. Использование такого языка изменяет взгляд на отношение между языком и действительностью. Обнаруживается, что буквы математического языка могут обозначать не только числа и фигуры, но и нечто гораздо более абстрактное (точнее, конструктное). Отсюда берет начало изобретение новых математических языков и диалектов, введение новых конструктов. Прецедент был создан Декартом. Фактически Декарт заложил основу описания явлений действительности с помощью формализованных символьных языков.
Непосредственное значение реформы Декарта заключалось в том, что она развязала руки математикам для создания в абстрактной символьной форме исчисления бесконечно малых, основные идеи которого в геометрической форме были известны еще древним. Если к дате выхода в свет «Геометрии» мы прибавим полвека, то очутимся в эпохе Лейбница и Ньютона, а еще через полвека — в эпохе Эйлера.
История науки показывает, что наибольшая слава достается обычно не тем, кто закладывает основы и, конечно, не тем, кто занимается мелкими заключительными доделками, а тем, кто в новом направлении мысли первым получает крупные результаты, поражающие воображение современников или ближайших потомков. Такую роль в европейской физико-математической науке сыграл Ньютон. Между тем известно высказывание Ньютона:
Если я видел дальше, чем Декарт, то потому, что я стоял на плечах Гигантов3.
Это, конечно, свидетельствует о скромности гениального ученого, но является также признанием долга перед первопроходцами со стороны «первополучателей». Яблоко, прославившее Ньютона, выросло на дереве, которое посадил Декарт.
1 Т. е. со сторонами, равными неравным частям.
2 Пробуждающаяся наука. Гл. 8.
3 If I have seen farther than Descartes, it is by standing on shoulders of giants.