Глава 9. Математика до греков
9.1. Ошибка природы
Мы уже приводили процесс счета в качестве примера использования модели действительности, которая не содержится в мозгу, а создается на уровне языка. И это очень яркий пример. Счет основан на способности расчленять окружающий мир на отдельные предметы. Эта способность возникла довольно давно в ходе эволюции; высшие позвоночные обладают ею, по-видимому, в такой же мере, как и человек. Ясно, что для успешной борьбы за существование живому существу, умеющему различать отдельные предметы, было бы небесполезно также уметь их считать (это помогло бы, например, ориентации в незнакомой местности). Описание с помощью чисел является естественным интегральным дополнением к дифференциальному описанию с помощью распознавания отдельных предметов. С другой стороны, кибернетический аппарат для распознавания чисел, т. е. для счета, может быть чрезвычайно простым. Эта задача гораздо более легкая, чем различение отдельных предметов. Поэтому можно было бы ожидать, что распознавание чисел в пределах, обусловленных устройством органов зрения, появится в ходе эволюции. Человеческий глаз может различать одновременно десятки и сотни отдельных предметов. Мы могли бы ожидать, что с одного взгляда будем также легко отличать совокупность из двухсот предметов от совокупности из двухсот одного, как два предмета отличаем от трех.
Однако природа не пожелала или не сумела дать нам этой способности. Непосредственно распознаваемые числа смехотворно малы — обычно до четырех — пяти. С помощью тренировки можно немного продвинуться вперед, но делается это путем мысленного разбиения на группы или запоминания картины в целом с последующим счетом в уме. Ограничение на непосредственное распознавание остается. Оно никак не связано с устройством органов зрения и обусловлено, очевидно, какими-то более глубинными особенностями строения мозга. Какими же? Пока не знаем. Одно обстоятельство заставляет задуматься и подсказывает некоторые предположения. Вот оно.
Кроме пространственного распознавания чисел, есть еще временное распознавание. Двойной стук в дверь мы никогда не спутаем с тройным или одинарным. Но восемь или десять ударов это уже заведомо «много», и различать такие звуки мы можем только по их суммарной продолжительности (это соответствует суммарной площади, занятой однородными предметами при пространственном распознавании). Предел, ограничивающий оба вида распознавания чисел, одинаков. Случайно ли это совпадение? Быть может, непосредственное распознавание чисел всегда имеет временную природу и ограничено емкостью мгновенной (оперативной) памяти — числом ситуаций, которые она вмещает. Ограничение на пространственное распознавание объясняется при этом предположении тем, что зрительное изображение развертывается во времени (при этом происходит быстрое переключение внимания с предмета на предмет, о чем говорилось выше) и подается для анализа на тот же самый аппарат.
Так или иначе, но в нашем мозговом устройстве природа оставила досадную недоделку и свою работу по созданию «продолжения мозга» человек начинает с исправления ее ошибки: он учится считать. Так начинается математика.
9.2. Счет и измерение
Факты убедительно свидетельствуют о том, что счет возникает раньше, чем названия чисел. Иначе говоря, первоначально языковыми объектами для построения модели служат не слова, а выделенные однотипные предметы: пальцы, камешки, узелки, черточки. Это и естественно. При возникновении языка слова связываются только с теми понятиями, которые уже существуют, т. е. распознаются. Слова «один», «два» и, возможно, «три» появляются независимо от счета (если понимать под счетом процедуру, протяженную во времени и осознаваемую как таковая), ибо они опираются на соответствующие нейронные понятия. Словам для больших чисел взяться неоткуда. Чтобы передать численность какой-то группы предметов, человек пользуется стандартными предметами, устанавливая между ними — один за другим — взаимно однозначное соответствие. Это и есть счет. Когда счет становится распространенным и привычным делом, для наиболее часто встречающихся (т. е. небольших) групп стандартных предметов возникают и словесные обозначения. На некоторых числительных остались следы их происхождения. Так, русское слово «пять» подозрительно похоже на старославянское «пядь» — рука (пять пальцев).
Есть первобытные народы, у которых всего два или три числительных: один, два, три. Все остальное — много. Но это вовсе не исключает умения считать с помощью стандартных предметов и передавать о численности путем разбиения на двойки и тройки или путем таких, не редуцированных еще выражений, как «столько, сколько пальцев на двух руках, одной ноге и еще один». Просто потребность в счете еще не так велика, чтобы заводить специальные слова. Последовательность «один, два, три, много» отражает не неспособность к счету до четырех и дальше, как иногда думают, а различие, которое проводит человеческий мозг между первыми тремя числами и всеми остальными. Ибо совсем без напряжения и бессознательно мы распознаем только числа до трех. Для распознавания четверки надо уже специально сосредоточиться. Так что не только для дикарей, но и для нас все, что больше трех, много.
Чтобы передать большие числа, люди стали считать «большими единицами» — пятерками, десятками, двадцатками.
Во всех известных нам системах счета большие единицы кратны пяти, что свидетельствует о том, что первым счетным инструментом всегда становились пальцы. Из комбинации больших единиц возникли еще большие единицы. В древнеегипетских папирусах встречаются отдельные иероглифы, изображающие числа до десяти миллионов.
Начало измерения, как и счета, относится к глубокой древности: мы находим его уже у первобытных народов. Измерение предполагает умение считать и требует дополнительно введения единицы измерения — меры измерительной процедуры, состоящей в сравнении измеряемого с единицей. Древнейшие меры связаны с человеческим телом: шаг, локоть, фут (ступня).
С возникновением цивилизации потребность в счете и в умении выполнять арифметические действия резко увеличивается. При развитом общественном производстве регулирование отношений между людьми: обмен, раздел имущества, налогообложение — требует знания арифметики и элементов геометрии. И мы находим эти знания в древнейших из известных нам цивилизаций — вавилонской и египетской.
9.3. Запись чисел
Запись чисел в древности (рис. 9.1) наглядно демонстрирует отношение к числу как к непосредственной модели действительности. Возьмем, например, египетскую систему. Она была основана на десятичном принципе и содержала иероглифы для единицы (вертикальная черточка) и «больших единиц». Чтобы изобразить число, надо было повторить иероглиф столько раз, сколько раз он входит в число. Аналогичным образом записывали числа другие народы древности. К этой простейшей форме записи примыкает и римская система. Она отличается лишь тем, что когда меньшая единица стоит слева от большей, ее надо не прибавлять, а отнимать. Это небольшое усовершенствование (вместе с введением промежуточных единиц: V, L, D) устранило необходимость выписывать подряд много одинаковых символов, и сделало римскую систему столь конкурентоспособной, что она существует и по сей день.
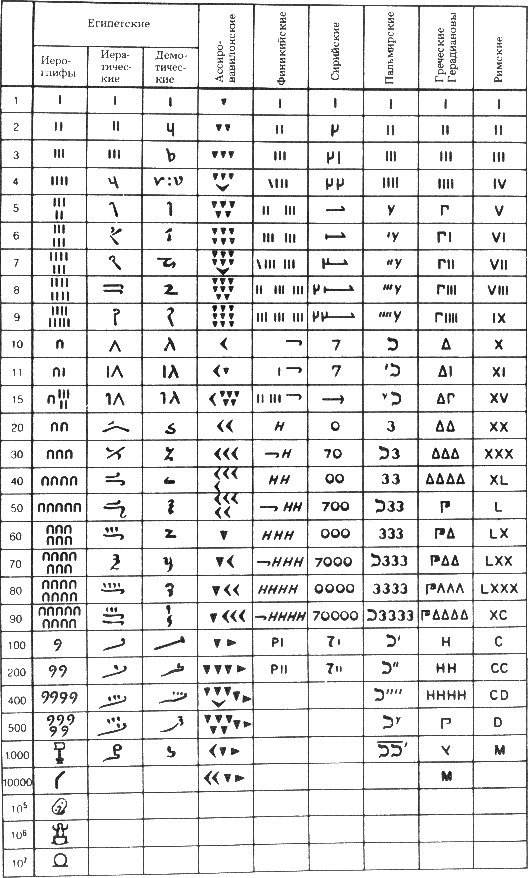
Рис.9.1. Запись чисел различными народами древности (из книги: Глейзер Г.И. История математики в школе. М., 1964)
Еще более радикальный способ избежать громоздкого повторения символов — это обозначить ключевые числа (меньше десяти, затем круглые десятки, сотни и т. д.) последовательными буквами алфавита. Так именно и поступили греки около VIII в. до н. э. Для единиц, десятков и сотен им хватило алфавита; числа, большие тысячи, изображались буквами со штрихом внизу слева. Так β обозначало 2, κ — 20, 'β — 2000. Эту систему переняли у греков многие народы: армяне, евреи, славяне и другие. При алфавитной нумерации «модельный» вид числа совершенно исчезает, оно становится просто символом. К тому же результату приводит и скорописное упрощение знаков, имеющих первоначально модельный вид.
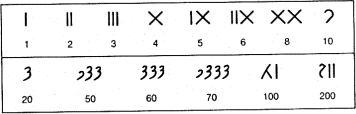
Рис. 9.2. Числовые знаки кхарошти
Современные европейские цифры, называемые в отличие от римских «арабскими», ибо они проникли к нам через арабов, имеют, как полагают, индийское происхождение. Не все специалисты соглашаются с этой гипотезой. В индийских письменных документах цифры встречаются впервые в III в. до н. э. В это время в ходу было два вида письма: кхарошти и брахми — и каждое из них имело свои числовые знаки (рис. 9.2 и 9.3). Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Вероятно, косой крест в качестве четверки соблазнил создателей чисел кхарошти простотой написания при полном сохранении модельности (четыре луча). Числовые знаки брахми более экономны. Считают, что первые девять знаков брахми породили в конечном счете современные цифры (рис. 9.4).

Рис. 9.3. Числовые знаки брахми
Утрата числами модельного вида с лихвой компенсировалась использованием в древнем мире абака — счетной доски с параллельными прорезями, по которым передвигались камешки. Разные прорези соответствовали единицам разного достоинства. Абак изобрели, вероятно, еще вавилоняне. Он служил для выполнения всех четырех действий арифметики. Греческие купцы широко пользовались абаком, того же типа счетные доски были в ходу у римлян. Латинское слово calculus (камешек) стало обозначать также «исчисление». Римляне же придумали надевать счетные камешки на рейки; так возникли счеты, которыми у нас пользуются и до сих пор. Эти простейшие счетные приборы имели большое значение, и только после того, как полностью сформировалась позиционная система счисления, они стали уступать место выкладкам на грифельной доске или бумаге.
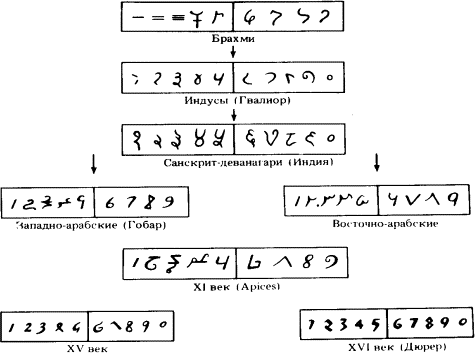
Рис. 9.4. Генеалогия современных цифр (по Menninger, Zahlwort, Ziffer)
9.4. Позиционная система
Основы позиционной системы заложили вавилоняне. В системе счисления, которую они заимствовали от своих предшественников — шумерийцев, мы с самого начала (т. е. в древнейших дошедших до нас глиняных табличках, относящихся к началу третьего тысячелетия до н. э.), видим две основные «большие единицы» — десять и шестьдесят. Откуда взялось число шестьдесят — об этом можно только догадываться. Известный историк математики О. Нейгебауэр полагает, что источником послужило отношение между основными денежными единицами, имевшими хождение в Двуречье: одна мана (по гречески мина) составляла шестьдесят шекелей. Такое объяснение не удовлетворяет нашего любопытства, ибо тотчас же возникает вопрос: а почему в мане шестьдесят шекелей? Не потому ли как раз, что в ходу была шестидесятиричная система? Ведь не потому мы считаем десятками и сотнями, что в рубле сто копеек! Ассириолог Ф.Тюро-Данжен приводит лингвистические аргументы в пользу того, что система счета была первичным явлением, а система мер — вторичным. Выбор числа шестьдесят был, очевидно, исторической случайностью, однако вряд ли можно усомниться, что этой случайности способствовала важная особенность числа шестьдесят: оно имеет необычайно много делителей: 2, 3, 4, 5, 6, 10, 12, 15, 20, 30. Это свойство очень полезно и для денежной единицы (с тех пор как существуют деньги, существует и деление их поровну), и для основания системы счета, если предположить, что какой-то мудрец ввел ее, руководствуясь соображениями удобства вычислений.
Математическая культура вавилонян известна нам по текстам, относящимся к двум периодам: древневавилонскому (1800–1600 гг. до н. э.) и эпохе Селевкидов (305–64 гг. до н. э.). Сравнение их показывает, что в математике вавилонян каких-либо радикальных перемен за эти полтора тысячелетия не произошло.
Вавилоняне изображали единицу узким
вертикальным клинышком ![]() , а
десять — широким горизонтальным
, а
десять — широким горизонтальным ![]() .
Число 35 выглядело так:
.
Число 35 выглядело так: ![]() .
Аналогично изображались числа до 59
включительно. Но 60 изображалось снова узким
вертикальным клинышком, таким же, как
единица! На самых древних табличках можно
видеть, что клинышек, изображающий 60, больше,
чем клинышек единицы. Таким образом, число 60
не только понималось как «большая единица»,
но и изображалось, в буквальном смысле
слова, как большая единица. Соответственно
появились «большие десятки» для
десятикратно увеличенных больших единиц.
Затем различие между большими и маленькими
клиньями стерлось, они стали
распознаваться по своему положению. Так
возникла позиционная система. Число 747 = 12
× 60 + 27 вавилонянин записал бы в виде:
.
Аналогично изображались числа до 59
включительно. Но 60 изображалось снова узким
вертикальным клинышком, таким же, как
единица! На самых древних табличках можно
видеть, что клинышек, изображающий 60, больше,
чем клинышек единицы. Таким образом, число 60
не только понималось как «большая единица»,
но и изображалось, в буквальном смысле
слова, как большая единица. Соответственно
появились «большие десятки» для
десятикратно увеличенных больших единиц.
Затем различие между большими и маленькими
клиньями стерлось, они стали
распознаваться по своему положению. Так
возникла позиционная система. Число 747 = 12
× 60 + 27 вавилонянин записал бы в виде: ![]() .
Числу 602 = 3600 соответствует третий
шестидесятиричный разряд и т. д. Но самое
замечательное, что таким же образом
вавилоняне изображали и дроби. В числе,
следовавшем за числом единиц, каждая
единица обозначала 1/60, в
следующем за ним числе — 1/3600 и т.
д. В современной десятичной записи мы
отделяем целую часть от дробной точкой или
запятой. Чем же отделяли целую часть от
дробной вавилоняне? Ничем! Число
.
Числу 602 = 3600 соответствует третий
шестидесятиричный разряд и т. д. Но самое
замечательное, что таким же образом
вавилоняне изображали и дроби. В числе,
следовавшем за числом единиц, каждая
единица обозначала 1/60, в
следующем за ним числе — 1/3600 и т.
д. В современной десятичной записи мы
отделяем целую часть от дробной точкой или
запятой. Чем же отделяли целую часть от
дробной вавилоняне? Ничем! Число ![]() могло с равным успехом обозначать и полтора
и девяносто. Та же неопределенность имела
место и в записи целых чисел: числа n, n
× 60, n × 602 и т. д. были
неотличимы. Множители или делители, кратные
шестидесяти, надо было добавлять по смыслу.
Так как 60 — довольно большое число, это к
особенным неприятностям не приводило.
могло с равным успехом обозначать и полтора
и девяносто. Та же неопределенность имела
место и в записи целых чисел: числа n, n
× 60, n × 602 и т. д. были
неотличимы. Множители или делители, кратные
шестидесяти, надо было добавлять по смыслу.
Так как 60 — довольно большое число, это к
особенным неприятностям не приводило.
Сравнивая вавилонскую позиционную систему с современной, мы видим, что неопределенность в множителе 60 — результат отсутствия знака нуль, который мы приписали бы нужное число раз в конце целого числа или начале дробного. Другим результатом отсутствия нуля является еще более серьезная неопределенность в интерпретации числовой записи, которая соответствует тому случаю, когда мы ставим нули в промежуточных разрядах. В самом деле, как отличить в вавилонской записи число 3601 = 1 × 602 + 0 × 60 + 1 от числа 61 = 1 × 60 + 1? Оба эти числа изображаются двумя единицами. Иногда неопределенность такого рода устранялась путем отодвижения чисел друг от друга с оставлением свободного места для недостающего разряда. Но этот метод не применялся систематически и во многих случаях большой пробел между числами ничего не означал. В астрономических таблицах эпохи Селевкидов встречается обозначение отсутствующего разряда с помощью знака, аналогичного нашей точке (разделитель фраз). В древневавилонскую эпоху ничего подобного мы не находим. Как же умудрялись древние вавилоняне избегать путаницы?
Полагают1, что разгадка состоит в следующем.
Ранние математические тексты вавилонян, дошедшие до нас, представляют собой сборники задач и их решений, созданные несомненно как учебные пособия. Их цель — обучить практическим приемам решения задач. Но ни в одном из текстов не описывается, как производить арифметические действия, в частности такие сложные для своего времени, как умножение и деление. Следовательно, предполагалось, что ученики каким-то образом умеют это делать. Так как совершенно невероятно, чтобы вычисления производились в уме, естественно предположить, что вавилоняне пользовались каким-то счетным прибором типа абака. На абаке числа выступают в своем натуральном, стихийно позиционном виде, а специальный знак для нуля не нужен, ибо бороздка, соответствующая пустому разряду, просто остается без камешков. Представление числа на абаке было основной формой задания числа, и в этом представлении не было никакой неопределенности. Числа, которые приводятся в клинописных математических текстах, играют роль поэтапных ответов, призванных контролировать правильность хода решения. Ученик делал выкладки на абаке и сверялся с глиняной табличкой. Ясно, что такому контролю отсутствие знака для пустых разрядов нисколько не препятствовало. Когда распространились объемистые астрономические таблицы, служащие уже не для контроля, а в качестве единственного источника данных, стали употреблять и разделительный знак для обозначения пустых разрядов. Однако свой «нуль» вавилоняне никогда не ставили в конце числа: очевидно, они его воспринимали именно как разделитель, но не как полноправное число.
Познакомившись с египетской и вавилонской системами записи дробей и действий над ними, греки для астрономических вычислений выбрали вавилонскую, ибо она была несравненно лучше. Но в записи целых чисел они сохранили свою алфавитную систему. Таким образом, греческая система, употреблявшаяся в астрономии, оказалась смешанной: целая часть числа изображалась в десятичной непозиционной системе, дробная часть — шестидесятиричной позиционной.
Не слишком логичное решение для создателей логики! С их легкой руки мы и до сих пор считаем часы и градусы (угловые) десятками и сотнями, а делим их на минуты и секунды.
Зато греки ввели в позиционную систему современный знак 0 — нуль, произведя его, как полагает большинство специалистов, от первой буквы слова ουδεν — «ничто». При записи целых чисел (кроме числа 0) этот знак, естественно, не находил применения, ибо алфавитная система, которой пользовались греки, не была позиционной.
Современную систему записи чисел изобрели индийцы в начале VI в.н.э. Вавилонский позиционный принцип и греческий знак нуль для обозначения пустоты они применили не к основанию 60, а к основанию 10. Система получилась и последовательной, и экономной, и не противоречащей традиции, и чрезвычайно удобной для вычислений.
Индийцы передали свою систему арабам. В Европе позиционная система счисления появилась в XVI в. с переводом знаменитой арабской арифметики ал-Хорезми (ал-Хваризми). Она вступила в жестокую борьбу с традиционной римской системой и в конце концов одержала победу. Однако еще в XVI в. в Германии был издан и выдержал много изданий учебник арифметики, в котором используются исключительно «немецкие», т. е. римские цифры, или, лучше сказать, числа, так как в то время цифрами называли только знаки индийской системы. В предисловии автор пишет: «Я изложил эту счетную книгу обычными немецкими числами на благо и пользу непосвященному читателю (которому сразу трудно будет выучить цифры)». Десятичные дроби в Европе стали употреблять начиная с Симона Стевина (1548–1620).
9.5. Прикладная арифметика
Магистральный путь к современной науке лежит через культуру древней Греции, которая наследовала достижения египтян и вавилонян. Остальные влияния и связи (в частности, передаточная функция, выполненная арабами) были более или менее существенны, но решающего значения, по-видимому, не имели. Истоки египетской и шумеро-вавилонской цивилизаций теряются во мраке первобытных культур. Поэтому в нашем обзоре истории науки мы ограничимся этими тремя культурами древности.
О записи чисел египтянами и вавилонянами
мы уже говорили. Надо только добавить
несколько слов о том, как египтяне
записывали дроби. Система их была с
современной точки зрения чрезвычайно
оригинальна и столь же неудобна. Египтяне
имели специальную форму записи только для
так называемых основных дробей, т. е.
полученных делением единицы на целое число,
и еще двух простых дробей, имевших с древних
времен особые иероглифы, а именно 2/3
и 3/4. Впрочем в позднейших
папирусах особое обозначение для 3/4
исчезло. Чтобы записать основную дробь,
надо было над обычным числом поставить знак
![]() , обозначающий «часть»,
Так
, обозначающий «часть»,
Так ![]() = 1/12.
= 1/12.
Остальные дроби египтяне разлагали на сумму нескольких основных дробей. Например, 3/8 записывалось как 1/4 + 1/8, а 2/7 в виде 1/4 + 1/28. Для результата деления 2 на 29 египетская таблица давала разложение 2/29 = 1/24 + 1/58 + 1/174 + 1/232.
На технике счета египтян и вавилонян мы останавливаться не будем. Достаточно сказать, что те и другие умели производить четыре действия арифметики над всеми числами (целыми, дробными или смешанными), которые встречались им на практике. Для действий с дробями они пользовались вспомогательными математическими таблицами; это таблицы обратных чисел у вавилонян и таблицы основных дробей — у египтян. Египтяне записывали промежуточные результаты на папирусе, вавилоняне, по-видимому, выполняли действия на абаке, поэтому детали их техники остались неизвестными.
Что же считали древние математики? Есть один отрывок из египетского папируса времен Нового Царства (1500–500 гг. до н. э.), в котором очень образно и с большой дозой юмора описывается деятельность царских писцов и который по этой причине неизменно приводится во всех книгах по истории математики. Не избежим и мы этой участи. Вот этот отрывок2:
Я хочу объяснить тебе, что это такое, когда ты говоришь: «Я, писец, дающий приказы армии»... Я ставлю тебя в тупик, когда приношу тебе повеление от твоего господина, тебе — его царскому писцу... мудрому писцу, поставленному во главе этого войска. Надо сделать наклонную насыпь в 730 локтей длины и 55 локтей ширины; она состоит из 120 отдельных ящиков и покрывается перекладинами и тростником. На верхнем конце она имеет высоту в 60 локтей, а в середине — 30 локтей. Уклон ее дважды по 15 локтей, а настил 5 локтей. Спрашивают у военачальников, сколько понадобится кирпичей, и у всех писцов, и ни один ничего не знает. Все они надеются на тебя и говорят: «Ты искусный писец, мой друг, сосчитай это для нас поскорей. Имя твое славится»... Сколько же нужно кирпичей?
Текст этот, несмотря на свою популярность, не слишком вразумителен. Однако, как бы мы его ни толковали, он дает представление о тех задачах, которые приходилось решать египетским писцам. Мы видим, в частности, что они должны были уметь вычислять (сколь верно — это другой вопрос) площади и объемы. И действительно, египтяне обладали некоторыми познаниями в геометрии. Эти познания, по весьма обоснованному мнению древних греков, возникли в самом Египте. Один из философов школы Аристотеля начинает свое сочинение словами3:
Так как нам необходимо здесь обозреть начало наук и искусств, то мы сообщаем, что геометрия, по свидетельству весьма многих, была открыта египтянами и возникла при измерении Земли. Это измерение было необходимо вследствие разлития реки Нила, постоянно смывавшего границы. Нет ничего удивительного, что эта наука, как и другие, возникла из потребностей человека. Всякое возникающее знание из несовершенного переходит в совершенное. Зарождаясь путем чувственного восприятия, оно постоянно становится предметом нашего рассмотрения и, наконец, делается достоянием нашего разума.
Деление знания на несовершенное и совершенное и определенная извинительная интонация по поводу «низкого» происхождения науки — это, конечно, от греческого философа. Египтяне, как и вавилоняне, не знали ничего подобного. Для них знание было чем-то вполне однородным. Они умели делать геометрические построения и знали формулы для площади треугольника и круга, как умели стрелять из лука и знали свойства целебных трав и даты разлива Нила. Геометрии как искусства выводить «истинные» формулы у них не было, она существовала, по выражению Б. Ван дер Вардена, лишь как раздел прикладной арифметики. Очевидно, при получении формул они использовали некоторые наводящие соображения, однако эти соображения мало кого интересовали. На отношение к формуле они не влияли.
9.6. Познания древних в геометрии
Что же знали египтяне из геометрии? — Правильные формулы для площади треугольника, прямоугольника, трапеции. Площадь неправильного четырехугольника, как можно судить по одному сохранившемуся документу, вычислялась так: полусумма двух противолежащих сторон умножалась на полусумму двух других противолежащих сторон. Формула эта грубо неверна (за исключением того случая, когда четырехугольник прямоугольный и когда она не нужна). Ни в каком разумном смысле ее нельзя назвать даже приближенной. Это, по-видимому, первый зафиксированный историей пример утверждения, которое выводится не из сравнения с опытными данными, а из «общих соображений». Площадь круга египтяне вычисляли, возводя в квадрат 8/9 его диаметра. Это соответствует приближенному значению числа π, отличающемуся примерно на 1% от истинного значения.
Объемы параллелепипедов и цилиндров вычислялись умножением площади основания на высоту. Высшим из известных нам достижений египетской геометрии является правильное вычисление объема усеченной пирамиды с квадратным основанием (Московский папирус). Оно следует формуле
V = (a2 + ab + b2) × h/3,
где h — высота, a и b — стороны верхнего и нижнего основания.
Наши сведения о познаниях древних вавилонян в математике скудны и отрывочны, но общее представление по ним все-таки составить можно.
Совершенно точно известно, что вавилоняне знали «теорему Пифагора», т. е., конечно, не теорему, а самый факт, что сумма квадратов катетов равна квадрату гипотенузы. Как и египтяне, они правильно вычисляли площади треугольников и трапеций. Длину окружности и площадь круга они вычисляли, пользуясь значением π = 3, что гораздо хуже, чем египетское приближение. Объем усеченной пирамиды или конуса вавилоняне вычисляли, умножая полусумму площадей оснований на высоту (неверная формула).
9.7. Арифметика с птичьего полета
Ситуации и представления в нервной системе человека моделируют смену состояний окружающей среды. Языковые объекты моделируют смену ситуаций и представлений. В результате теория является «двухэтажной» языковой моделью действительности (рис. 9.5). Схема использования теории такова. Ситуация Si кодируется языковым объектом Li. Этот объект, конечно, может состоять из множества других объектов и иметь сколь угодно сложную структуру. Объект L1 есть имя для S1. Некоторое время спустя ситуация S1 сменяется ситуацией S2. Осуществляя некоторую языковую деятельность, мы преобразуем L1 в другой объект L2, и, если наша модель правильна, L2 есть имя S2. Тогда, не зная реальной ситуации S2, мы можем получить о ней представление путем декодирования языкового объекта L2. Языковая модель определяется, очевидно, как семантикой объектов Li («материальная часть» по военной терминологии), так и видом языковой деятельности, превращающей L1 в L2.
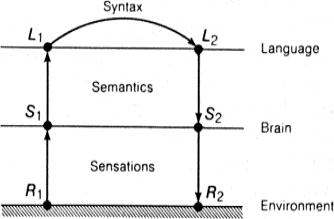
Рис. 9.5. Двухэтажная языковая модель действительности
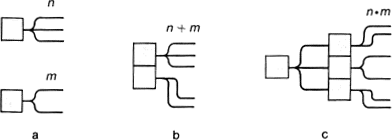
Рис. 9.6. Действия над целыми числами
Заметьте, что мы ничего не сказали о «выделении существенных сторон явления», о «причинно-следственной связи» и прочих подобных вещах, которые обычно красуются на почетных местах при описании сущности научного моделирования. И ситуация S1 у нас «не порождает» ситуацию S2, а лишь «сменяется» ею. Это, конечно, не случайно. Нарисованная нами схема логически предшествует упомянутым философским понятиям. Если у нас есть языковая модель, и лишь постольку, поскольку она у нас есть, мы можем говорить о существенных сторонах явления, об идеализации, о причинно-следственной связи и т. п. Все эти понятия, хотя они по внешности предстают как условия создания языковой модели, на самом деле являются лишь описанием в общих терминах (конечно, очень важным и нужным) уже существующих моделей. Хотя эти понятия как-будто бы «объясняют», почему вообще может существовать языковая модель, на самом деле они сами являются элементами языковой модели следующего уровня (иерархии по управлению) и исторически, конечно, появляются позже, чем первичные языковые модели (например, арифметические). Поэтому, прежде чем использовать эти понятия, мы должны констатировать, что языковые модели вообще существуют. И на этом уровне описания нам нечего добавить к схеме на рис. 9.5. «Так бывает» — вот и все.
Как же создаются и развиваются теории? Как и все в мире, по методу проб и ошибок. Если есть отправная точка, то, начиная от нее, человек принимается сооружать языковые конструкции и исследовать, что у него получилось. Фазы конструирования и исследования постоянно сменяют друг друга: конструкция порождает исследование, исследование порождает новые конструкции.
Отправной точкой арифметики является понятие числа (целого). Аспект действительности, который отражает это понятие таков: отношение целого к его частям, способ разложения целого на части. Ту же самую мысль можно выразить и с противоположной стороны: число — способ объединения частей в целое, т. е. в некое множество (конечное). Два числа считаются тождественными, если части (элементы множества) можно поставить во взаимно однозначное соответствие; в установлении этого соответствия и состоит счет. Очевидно, однако, что одних чисел мало для теории, необходимы еще действия над ними — элементы функционирования модели, преобразования L1 → L2. Возьмем два числа n и m и представим их схематически как два способа разложения целого на части (рис. 9.6,a).
Как из этих двух чисел получить третье, т. е. третий способ разложения целого на части? Сразу приходит на ум два способа, которые можно назвать параллельным и последовательным соединением разложений. При параллельном способе оба целых образуют в качестве частей новое целое (рис. 9.6,b). Это разложение (число) мы назовем суммой двух чисел. При последовательном способе мы берем одно из разложений и каждую его часть разлагаем в соответствии с другим разложением (рис. 9.6,c). Новое число называется произведением. Оно не зависит от порядка производящих чисел. Это очень хорошо видно, если интерпретировать действия над числами не как соединение разложений, а как образование нового множества. Сумма есть, очевидно, результат слияния двух множеств в одно (объединение множеств). Произведение имеет своим прообразом множество сочетаний любого элемента первого множества с любым элементом второго (такое множество называется в математике прямым произведением множеств). Связь этого определения с предыдущим можно проследить таким образом. Пусть первое разложение делит целое A на части a1, a2, ..., an, второе делит B на части b1, b2, …, bm. Сделав первое разложение, пометим буквами ai полученные части. Разлагая каждую часть второго на части bi сохраним первую букву и добавим вторую. Значит, на каждой части результата будет стоять aibj и все эти сочетания будут разные. Подходы от целого к части и от части к целому дополняют друг друга. Из рис. 9.6,c легко увидеть также, что умножение можно свести к повторному сложению.
Конечно, древний человек, создавая арифметику, был далек от этих рассуждений. Но ведь и лягушка не знала, что ее нервная система должна быть устроена по иерархическому принципу! Важно, что это знаем мы.
Имея языковые объекты, изображающие числа, и умея производить над ними сложение и умножение, мы уже получаем теорию, дающую нам работающие модели действительности. Разберем простейший пример, поясняющий схему на рис. 9.5.
Пусть некий земледелец засеял пшеницей поле длиной в 60 шагов и шириной 25 шагов. Допустим, что он ожидает урожая в одну кружку пшеницы с квадратного шага. Прежде чем приступать к уборке, он хочет знать, сколько он получит кружек пшеницы. Здесь S1 — ситуация перед уборкой пшеницы, включающая, в частности, результат измерения длины и ширины поля в шагах и ожидаемую урожайность; S2 — ситуация после уборки, включающая, в частности, результат измерения количества пшеницы кружками; L1 — языковый объект 60 ×25 (знак умножения является таким же отражением ситуации S1, как числа 60 и 25: он отражает структуру множества квадратных шагов на плоскости как прямого произведения множеств линейных шагов в длину и ширину); L2 — языковый объект 1500.
Терминологическое замечание. Под теорией мы понимаем просто языковую модель действительности, дающую нечто новое по сравнению с нейронными моделями. В этом определении не учитывается, что теории могут образовывать иерархию по управлению, да этот факт и трудно отразить без введения математического аппарата. Более общие модели могут порождать более частные модели. Теорию и языковую модель мы будем считать синонимами, но все же, когда речь идет о порождении одной модели другой моделью, мы более общую будем называть теорией, а более частную — моделью.
9.8. Обратный ход модели
Фаза исследования только что созданной теории включает деятельность по двум направлениям. Первое — это всесторонняя проверка теории, сравнение ее с опытом, поиск изъянов. Но допустим, теория хороша. Тогда на первый план выступает второе направление — попытка дать модели «обратный ход», т. е. по заданному L2 определить те или иные особенности L1. Эта процедура отнюдь не лишена практического смысла. Человек использует модель для планирования целенаправленной деятельности, он хочет знать, что ему надо делать, чтобы получить требуемый результат, какое должно быть L1, чтобы получить данное L2. В нашем примере с земледельцем вопрос может быть поставлен, например, так: при известной ширине поля какова должна быть его длина, чтобы получить заданное количество пшеницы?
Однако не всегда исследование обратного хода модели диктуется сиюминутными потребностями практики. Часто это делается из чистого любопытства, по принципу «интересно, что получится?» Тем не менее, результатом такой деятельности будет лучшее понимание устройства и свойства модели и создание новых конструкций и моделей, т. е., в конечном счете, многократно увеличенная польза для практики. В этом состоит высшая мудрость природы, наделившей человека «чистым» любопытством.
В арифметике обратный ход модели приводит к понятию уравнения. Простейшие уравнения порождают операции вычитания и деления. Пользуясь современным алгебраическим языком, мы определяем разность b - a как решение уравнения a + x = b, т. е. такое число x, что это равенство становится верным. Аналогично определяется частное от деления b на a. Операция деления порождает новую конструкцию — дробь. Повторное умножение числа на самое себя порождает конструкцию степени, а обратный ход при наличии этой конструкции — операцию извлечения корня. Это завершает перечень арифметических конструкций, которые были в употреблении у древних египтян и вавилонян.
9.9. Решение уравнений
С развитием техники счета и вообще с развитием цивилизации стали появляться и решаться все более сложные уравнения. Древние не знали, конечно, современного алгебраического языка, они выражали уравнения на обычном разговорном языке подобно тому, как это делается в наших школьных учебниках арифметики. Но это не меняет сущности задач, которые они решали (и так называемых арифметических школьных задач), как задач на решение уравнений.
Величину, подлежащую определению, египтяне называли «аха», что переводят как «некоторое количество» или «куча». Вот пример формулировки задачи из египетского папируса: «количество и его четвертая часть дают вместе 15». Это задача «на части» по современной арифметической терминологии, а на алгебраическом языке она соответствует уравнению
x + 1/4 x = 15.
Приведем пример более сложной задачи египетских времен.
Квадрат и другой квадрат, сторона которого есть 1/2 + 1/4 стороны первого квадрата, имеют вместе площадь 100. Вычисли мне это.
Решение в современных обозначениях:
x2 + (3/4 x)2 = 100, (1 + 9/16) x2 = 100,
5/4 x = 10, x = 8, 3/4 x = 6,
Описание решения в папирусе:
Возьми квадрат со стороной 1 и возьми 1/2 + 1/4 от 1, т. е. 1/2 + 1/4 в качестве стороны второй площади. Помножь 1/2 + 1/4 на самое себя, это дает 1/2 + 1/16. Поскольку сторона первой площади взята за 1, а второй за 1/2 + 1/4, то сложи обе площади вместе; это дает 1 + 1/2 + 1/16. Возьми корень отсюда: это будет 1 + 1/4. Возьми корень из данных 100: это будет 10. Сколько раз входит 1 + 1/4 в 10? Это входит 8 раз.
Дальше текст не сохранился, но конец очевиден: 8 × 1 = 8 — сторона первого квадрата, 8 × (1/2 + 1/4) = 6 — второго.
Египтяне умели решать только линейные и простейшие квадратные уравнения с одним неизвестным. Вавилоняне продвинулись гораздо дальше. Вот пример задачи из вавилонских текстов.
Площади двух моих квадратов я сложил: 25 25/60. Сторона второго квадрата равна 2/3 стороны первого и еще 5.
Далее следует совершенно правильное ее решение. Эта задача эквивалентна системе уравнений с двумя неизвестными:
x2 + y2 = 25 25/60, y = 2/3 x + 5.
Вавилоняне умели решать полное квадратное уравнение
x2 ± ax = b,
кубические уравнения
x3 = a и x2 (x + 1) = a,
системы уравнений, подобные приведенной выше, а также вида
x2 ± y = a, xy = b.
Кроме того, они пользовались формулами
(a + b)2 = a + 2ab + b2 и (a + b)(a - b) = a2 - b2,
умели суммировать арифметические прогрессии, знали суммы некоторых числовых рядов и числа, которые впоследствии подучили название пифагоровых (такие целые числа x, y, z, что х2 + у2 = z2).
9.10. Формула
Место древнего Египта и Вавилона в истории математики можно определить следующим образом: в этих культурах впервые появилась формула. Под формулой мы понимаем не только буквенно-цифровое выражение современного алгебраического языка, но вообще всякий языковый объект, являющийся точным (формальным) предписанием, как производить преобразование L1 → L2 или какие-либо вспомогательные преобразования в рамках языка. Формулы представляют собой важнейшую часть любой развитой теории, хотя, конечно, не исчерпывают ее, ибо в теорию входит еще семантика языковых объектов Li. Утверждение о связи между величинами сторон в прямоугольном треугольнике, содержащееся в теореме Пифагора, — это формула, если даже оно выражено словами, а не буквами. Типовая задача с описанием хода решения («делай так!») и с примечанием, что числа могут быть произвольны (это может быть не высказано, но подразумеваться), — это тоже формула. Именно такие формулы и дошли до нас в египетских папирусах и на вавилонских глиняных табличках.
1 См. замечания И.Н. Веселовского к переводу книги: Ван дёр Варден Б. Пробуждающаяся наука. М.: Физматгиэ, 1959.
2 C небольшими сокращениями.
3 Этот отрывок дошел до нас через Прокла (V в.н.э) — комментатора Евклида.