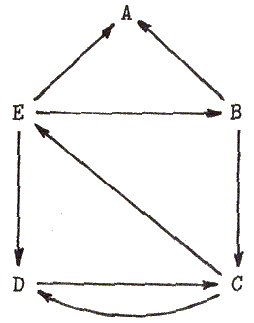
Рисунок 5.1 Ориентированный граф
5. РАЗРАБОТКА ПРОГРАММ
В этой главе приводится ряд примеров разработки программ на РЕФАЛе.
| 5.1. Миссионеры и каннибалы |
| 5.2. Алгоритмы сортировки |
| 5.3. Пути на графе |
| 5.4. Трансляция арифметических выражений |
РЕФАЛ является таким языком, который ориентирован на конструирование определенных объектов , представленных РЕФАЛ-выражениями, и на манипулирование ими. Структура управления РЕФАЛ-программы весьма проста и незамысловата: сопоставление в образцом и подстановка. Именно структура объектов, которыми манипулирует программа, несет бремя хранения всей полезной информации. Удачное программирование на РЕФАЛе - это прежде всего удачный выбор основных структур данных. Представление проблемы, которая должна быть решена, в терминах РЕФАЛ-выражений является первой и важнейшей частью программирования на РЕФАЛе. Это представление должно, во-первых, быть наглядным для человека, во-вторых, допускать выражение основных операций над данными в терминах трансформации объектов в соответствии с некоторыми простыми образцами. Если эти два требования удовлетворяются, у вас достаточно хорошие шансы написать РЕФАЛ-программу, которая будет компактной, читаемой, и в то же время легко отлаживаемой.
Рассмотрим хорошо известную задачу "Миссионеры и каннибалы''. Три миссионера и три каннибала приходят на берег реки и видят лодку. Они хотят переплыть реку. Лодка, однако, не может вместить более двух человек. Дальнейшим ограничением является следующее. Ни в один момент времени число каннибалов на любом берегу реки (включая причалившую лодку) не должно превосходить число миссионеров (так как в этом случае миссионеров одолеют и съедят). Каким образом можно переплыть реку (если это вообще возможно ) ?
Общий метод решения задачи таков:
Как будут представлены ситуации в нашей задаче? Подвыражения в РЕФАЛе представляют подсистемы в полной системе. Наша система очевидным образом включает две подсистемы людей: находящихся на левом и на правом берегу реки. Таким образом, можно использовать образец:
(e.Left-bank)(e.Right-bank)
Простейшие объекты могут быть представлены РЕФАЛ-символами. Будем использовать для обозначения миссионера 'M' , а для каннибала -'C'. Ситуация, когда на левом берегу три миссионера и один каннибал, а на правом берегу два каннибала, может быть тогда представлена следующим образом:
('MMMC')('CC')
Так как порядок, в котором люди перечисляются, не играет роли, три миссионера и каннибал могут быть также представлены как 'CMMM' , 'MCMM' , и т.д. Нужно ли оставлять такую свободу в представлении или лучше фиксировать определенный порядок? Последний вариант, очевидно, предпочтительнее. Следует продумать заранее использование РЕФАЛ-представлений в образцах. При произвольном порядке символов для определения, находятся ли миссионеры на данном берегу, будет использоваться образец e1'M'e2 . Этот образец включает открытую e-переменную, которая означает просмотр выражения. Если принять соглашение о перечислении миссионеров перед каннибалами, то же самое может быть определено по более простому образцу 'M'e1 . Чтобы определить, имеется ли в группе хотя бы один каннибал, применяется e1'C' , а для определения, присутствуют ли в ней оба вида людей, применяется 'M'e1'C'. Здесь используется тот факт, что люди делятся только на два вида.
Теперь следует позаботиться о лодке. Один из способов - включить ее в качестве символа 'B' в описание соответствующего берега, скажем, так:
('MMMC')('BCC')
Однако, это будет не слушком удобно. Чтобы абстрагироваться от размещения лодки, будут применяться два образца:
('B'e1)(e2) = (e1)(e2);
(e1)('B'e2) = (e1)(e2);
Лодка не будет приравниваться к людям; ее расположение является независимым измерением. Более хорошая идея - добавлять один символ ('L' или 'R') - для того, чтобы отмечать, находится ли лодка на левом или на правом берегу. Допустим, что вся компания приходит на левый берег реки. Тогда представлением начальной ситуации (состояния) служит:
L(e.Left-bank)(e.Right-bank)
ЗАМЕЧАНИЕ: Для представления миссионеров и каннибалов были использованы символы (обратите внимание на кавычки), а для положения лодки - идентификаторы L и R . Это не имеет большого значения. Обычно программа выглядит лучше, если элементы, которые могут образовать предложение, представлены символами, в то время как символы, используемые отдельно, представлены идентификаторами.
Обратимся теперь ко множеству возможных
перемещений. Перемещением является переплывание
реки на лодке. Так как лодка может вместить не
более двух человек и не может переплывать сама,
то имеется пять возможных перемещений, которые
будут представлены последовательными номерами в
следующей таблице:
| Перемещение | В лодку садятся: |
| 1 | два миссионера |
| 2 | два каннибала |
| 3 | миссионер и каннибал |
| 4 | миссионер |
| 5 | каннибал |
Не все перемещения физически возможны в каждом состоянии. Например, если лодка находится на левом берегу и только один миссионер на этом берегу, тогда перемещение 1 невозможно. Но даже если перемещение возможно, следует проверить, является ли оно допустимым, т.е. не приводит ли к убийству. Так как перемещение является трансформацией текущего состояния, то оно определяется как:
* Move
* <Move s.Move e.State> == s.New-State
Move { sM eS = <Admiss <Try sM eS>>; }
Функция Try будет трансформировать состояние. Если перемещение невозможно в данном состояниия, то новое, фиктивное, состояние будет представляться символом Imposs. Admiss будет проверять, что результирующее состояние удовлетворяет необходимым требованиям. Если это так, функция оставит состояние неизменным. Если же требования не удовлетворяются, она заменит состояние на Imposs . Вот как выглядит простое и прямолинейное определение Try, которое использует средства сопоставления с образцом языка РЕФАЛ и изобилует комментариями:
* Try a move
Try {
* Boat on left bank
* MM crossing
1 L('MM'e1)(e2) = R(e1)('MM'e2);
* CC crossing
2 L(e1'CC')(e2) = R(e1)(e2'CC');
* MC crossing
3 L(e1'MC'e2)(e3) = R(e1 e2)('M'e3'C');
* M crossing
4 L('M'e1)(e2) = R(e1)('M'e2);
* C crossing
5 L(e1'C')(e2) = R(e1)(e2'C');
* Boat on right bank
* MM crossing
1 R(e1)('MM'e2) = L('MM'e1)(e2);
* CC crossing
2 R(e1)(e2'CC') = L(e1'CC')(e2);
* MC crossing
3 R(e1)('M'e2'C') = L('M'e1'C')(e2);
* M crossing
4 R(e1)('M'e2) = L('M'e1)(e2);
* C crossing
5 R(e1)(e2'C') = L(e1'C')(e2);
* Otherwise move impossible
s.Mv eS = Imposs;
}
Функция приемлемости проверяет, что условие "непоедания'' выполняется на каждом берегу:
* Admissibility of the move
Admiss {
s.Side(eL)(eR),
<No-eat eL>: T, <No-eat eR>: T =
s.Side(eL)(eR);
eS = Imposs;
}
* No eating missionaries
No-eat {
*1. Both missionaries and cannibals are present
'M'e1'C' = <Compare e1>;
* Otherwise OK
e1 = T; }
* Both M and C on the bank.Compare the numbers.
Compare {
'C'e1 = F;
'M'e1'C' = <Compare e1>;
e1 = T; }
Дерево достижимых состояний содержит узлы-состояния и ребра-перемещения. Перемещение и состояние, в которое оно ведет, могут быть легко объединены в единый элемент, который будет называться связью:
(s.Move'='e.State)
где знак равенства вставлен просто для удобочитаемости. Чтобы подогнать начальное состояние под этот формат, будем рассматривать его как следующее из фиктивного предшествующего перемещения со специальным кодом . Дерево состояний начинается следующим образом:
(0 = Sinit)(1 = S1)(1 = S11)...
(2 = S12)...
...
(5 = S15)...
(2 = S2)(1 = S21)...
(2 = S22)...
...
Примем в качестве метода поиска по дереву метод "внутри-слева" и простой фиксированный порядок опробования перемещений: 1, 2, и т.д. до 5. Тогда на самом деле нет надобности работать со всей структурой дерева. Можно хранить только одну цепочку связей, которая образует путь из корня в текущий узел.
Назовем поисковую функцию Search . Она вызывается в начале программы с начальной цепочкой в качестве аргумента:
$ENTRY Go { =
<Search (0'='L('MMMCCC')())>; };
Теперь желательно рассмотреть все случаи, которые могут встретиться в ходе поиска.
Задача считается решенной, когда состояние в последней связи является целевым. Имеем предложение:
e1 (s.M'='R()('MMMCCC')) =
<Path e1 (s.M'='R()('MMMCCC'))>;
В этом случае остается только подходящим образом напечатать решение, что является обязанностью функции Path .
Это предложение будет испытываться первым. Пока оно не срабатывает, продолжается поиск и удлинение нашего пути за счет добавления новой связи, возникающей в результате перемещения 1 :
e1 (sM'='eS) =
<Search e1 (sM'='eS) (1'='<Move 1 eS>)>;
Теперь, если этот путь записать, видно, что последним состоянием в пути может оказаться Imposs . Поэтому, перед удлинением пути следует проверять, является ли последнее состояние допустимым или состоянием Imposs , и в последнем случае предпринять соответствующее действие. Как всегда в РЕФАЛе, предложение (или предложения) для специального случая, когда eS является Imposs, должно предшествовать предложению (ям) для общего случая.
Если результатом последнего перемещения является Imposs , испытывается следующее перемещение, т.е., последняя связь замещается следующим образом:
e1 (s.Mp'='eS)(s.M'='Imposs), <+ s.M 1>: s.Mn = <Search e1 (s.Mp'='eS) (s.Mn'='<Move s.Mn eS>)>;
Это подразумевает, обднако, что s.M меньше, чем 5. Если оно совпадает с 5, то это означает, что в нашем распоряжении больше нет перемещений, и следует совершить возврат, т.е., удалить последнюю связь и предпринять следующее (возможное) перемещение в предыдущей связи. Для того, чтобы совершить следующее перемещение в предыдущей связи в соответствии с общим правилом, состояние в этой связи заменяется на Imposs :
e1 (s.Mp'='eS) (5'='Imposs) = <Search e1 (s.Mp'='Imposs)>;
По написанному РЕФАЛ-предложению, т.е. правилу замещения, можно произвести анализ, чтобы увидеть, каковы возможные исключения из него. Мы уже использовали этот метод выше и должны применить его опять. Если предшествующая связь является начальной связью, т.е. s.Mp является равным 0, то нет возможности для возврата и следует объявить, что задача не имеет решения:
(0'='eS) (5'='Imposs) = <Prout 'The problem has no solution'>;
Имеется еще одна ситуация, подлежащая рассмотрению. Когда достигается состояние, которое уже было пройдено прежде, т.е. может быть обнаружено в одной из связей построенного пути, нежелательно просматривать его продолжения, поскольку они уже были просмотрены в качестве продолжений предыдущего вхождения этого состояния. Таким образом, повторяющееся состояние замещается на Imposs :
e1 (s.Mp'='eS) e2 (s.M'='eS) = <Search e1 (s.Mp'='eS) e2 (s.M'='Imposs)>;
Теперь следует собрать все шесть предложений в правильном порядке. Совместно с другими функциональными определениями (предоставляем читателю изобразить, как работает функция Path ), образуем следующую программу:
* Missionaries and Cannibals
$ENTRY Go { =
<Search (0'='L('MMMCCC')())>; };
Search {
*1. The goal found
e1 (s.M'='R()('MMMCCC')) =
<Path e1 (s.M'='R()('MMMCCC'))>;
*2. Impossible state. No backup. No solution.
(0'='eS) (5'='Imposs) =
<Prout 'The problem has no solution'>;
*3. Impossible state. No next move. Back up.
e1 (s.Mp'='eS) (5'='Imposs) =
<Search e1 (s.Mp'='Imposs)>;
*4. Impossible state. Do next move.
e1 (s.Mp'='eS)(s.M'='Imposs),
<+ s.M 1>: s.Mn =
<Search e1 (s.Mp'='eS)
(s.Mn'='<Move s.Mn eS>)>;
*5. Repeated state. Equate to impossible.
e1 (s.Mp'='eS) e2 (s.M'='eS) =
<Search e1 (s.Mp'='eS) e2 (s.M'='Imposs)>;
*6. Down the tree.
e1 (s.M'='eS) =
<Search e1 (s.M'='eS) (1'='<Move 1 eS>)>;
}
* Move
Move { eS = <Admiss <Try eS>>; }
* Try a move
Try {
* Boat on left bank
* MM crossing
1 L('MM'e1)(e2) = R(e1)('MM'e2);
* CC crossing
2 L(e1'CC')(e2) = R(e1)(e2'CC');
* MC crossing
3 L(e1'MC'e2)(e3) = R(e1 e2)('M'e3'C');
* M crossing
4 L('M'e1)(e2) = R(e1)('M'e2);
* C crossing
5 L(e1'C')(e2) = R(e1)(e2'C');
* Boat on right bank
* MM crossing
1 R(e1)('MM'e2) = L('MM'e1)(e2);
* CC crossing
2 R(e1)(e2'CC') = L(e1'CC')(e2);
* MC crossing
3 R(e1)('M'e2'C') = L('M'e1'C')(e2);
* M crossing
4 R(e1)('M'e2) = L('M'e1)(e2);
* C crossing
5 R(e1)(e2'C') = L(e1'C')(e2);
* Otherwise move impossible
s.M eS = Imposs;
}
* Admissibility of the move
Admiss {
s.Side(eL)(eR), <Noeat eL>:T, <Noeat eR>:T =
s.Side(eL)(eR);
eS = Imposs;
}
* No eating missionaries
Noeat {
*1. Both missionaries and cannibals are present
'M'e1'C'= <Compare e1>;
* Otherwise OK
e1 = T; }
* Both M and C on the bank.Compare the numbers.
Compare {
'C'e1 = F;
'M'e1'C'= <Compare e1>;
e1 = T; }
* Print the path leading to the goal
Path {
(0'='eS) e2 =
<Prout 'The initial state: 'eS>
<Path e2>;
(s.M'='s.Side eS) e2,
<Look-up s.M In <Table>>: e.Who =
<Prout e.Who ' crossing to 's.Side
' bank: state ' s.Side eS>
<Path e2>;
= ;
}
Look-up { sM In e1 sM(e.Who) e2 = e.Who }
Table { =
1('MM') 2('CC') 3('MC') 4('M ') 5('C ') }
Назовем файл этой программы mmmccc.ref . Транслируем его посредством refc и запускаем:
refgo mmmccc -nt
(указанные флажки приводят к выдаче на печать номера шага РЕФАЛ-машины и затраченного на шаг времени). Вывод имеет вид:
The initial state: L (MMMCCC)() CC crossing to R bank: state R (MMMC)(CC) C crossing to L bank: state L (MMMCC)(C) CC crossing to R bank: state R (MMM)(CCC) C crossing to L bank: state L (MMMC)(CC) MM crossing to R bank: state R (MC)(MMCC) MC crossing to L bank: state L (MMCC)(MC) MM crossing to R bank: state R (CC)(MMMC) C crossing to L bank: state L (CCC)(MMM) CC crossing to R bank: state R (C)(MMMCC) M crossing to L bank: state L (MC)(MMCC) MC crossing to R bank: state R ()(MMMCCC)
Упражнение 5.1 * Усилия, которые нужно затратить на поиск решения (как и само решение) зависят от порядка, в котором испытываются возможные перемещения. До этого был использован один и тот же порядок перемещений, независимо от того, на каком берегу находится лодка. Однако, эти порядки могут отличаться. Модифицировать программу, изменяя порядок перемещений таким образом, чтобы она выполнялась быстрее или медленнее, чем данная программа.
Пусть задан предикат Order, который вводит отношение (полного) порядка на некотором множестве РЕФАЛ-термов; так, <Order t1 t2> принимает значение T , если пара t1 t2 упорядочена должным образом, и значение F в противном случае. Отношение порядка рефлексивно, антисимметрично и транзитивно.
Имея такое отношение, можно задаться целью упорядочить данный список термов таким образом, чтобы в любом случае, когда t1 предшествует t2 в списке, <Order t1 t2> являлся истинным. В программировании такая процедура упорядочивания обычно называется сортировкой. Термы, подлежащие упорядочиванию, могут, например, быть заключенными в скобки строками, для которых в качестве Order выступает лексикографическое отношение, либо числами с Order, которое является отношением "меньше или равно".
Наиболее очевидным способом упорядочивания последовательности термов является перeстановка соседних термов до тех пор, пока они не удовлетворят отношению порядка:
* Definition of sorting
Sort {
e1 tX tY e2, <Order tX tY>: F =
<Sort e1 tY tX e2>;
e1 = e1; }
Эта функция является хорошим пояснением к проблеме, однако в качестве ее решения чрезвычайно неэффективна. В самом деле, предположим, выполнен шаг РЕФАЛ-машины, при котором поменялись местами tX и tY . Теперь все соседние пары в e1 tY , за исключением, быть может, последней (образованной за счет последнего терма в e1 и tY ), должны удовлетворять отношению порядка. Тем не менее, на следующем шаге РЕФАЛ-машина станет проверять все эти пары перед тем, как она дойдет до следующей неупорядоченной пары.
Улучшение напрашивается само собой: заключить уже готовую часть в круглые скобки и сравнивать последний терм готовой (упорядоченной) части с первым термом еще неупорядочивавшейся части:
Sort {
= ;
sX e2 = <Sort1 (sX) e2>; }
Sort1 {
(e1 tX) tY e2, <Order tX tY>:
{ T = <Sort1 (e1 tX tY) e2>;
F = <Sort1 (e1) tY tX e2>;
};
(e1) = e1; }
Этот алгоритм значительно лучше, но его можно еще улучшить. После перестановки sX и sY готовая часть e1 укорачивается на один терм, и это будет продолжаться до тех пор, пока sY не окажется неупорядоченным по отношению к последнему терму e1 . Однако, когда sY займет свое место, вся первоначальная часть e1 будет упорядочена; поэтому можно улучшить алгоритм за счет восстановления исходного положения круглых скобок. Конечно, это не может быть проделано, если не зафиксировать каким-либо образом их положение в начале процесса. Так мы приходим к алгоритму, который известен как сортировка вставками: сохранение правильного порядка в начальной части списка и вставка каждого следующего терма в соответствующее место путем перемещения его справа налево:
* Insertion sort
Sort {e1 = <Sort1 ()e1>; };
Sort1 {
(e1) tY e2 = <Sort1 (<Insert e1 tY>) e2>;
(e1) = e1; }
* <Insert e1 tY> assumes that e1 is ordered
* and inserts tY into it
Insert {
e1 tX tY, <Order tX tY>:
{T = e1 tX tY;
F = <Insert e1 tY> tX;
};
e1 = e1;
};
При использовании этого алгоритма среднее количество шагов, необходимых для того, чтобы отсортировать n термов, равно приблизительно n2 / 2. Имеются алгоритмы, такие как сортировка слиянием, которые проделывают то же за количество шагов, пропорциональное n log n . Идея сортировки слиянием состоит в делении и выборе. Для того, чтобы отсортировать список, его делят на две приблизительно равные части. Затем эти части сортируются каждая по отдельности и сливаются в один отсортированный список. Во время слияния двух упорядоченных списков ни один из них не нужно просматривать повторно. Просто сравниваются первые элементы обоих списков и выбирается наименьший (точнее, не превосходящий другого). Таким образом, общее количество операций при слиянии будет пропорционально n. Для того, чтобы отсортировать половины первоначального списка, их делят на четверти, и т.д. Так как общее количество термов на всех уровнях деления всегда равно n, то время, требуемое для всех слияний, на каждом уровне пропорционально n. Число уровней деления, необходимое для того, чтобы прийти к одноэлементному списку, равно log n. Отсюда общее время сортировки составляет n log n.
В реализации этой идеи лучше идти от противного: сперва сформировать двухтермовые упорядоченные списки, затем слить их в четырехтермовые списки, и т.д.:
* Merge-sort
Sort { e1 = <Check <Merge <Pairs e1>>>; };
* Form ordered pairs from a list of terms
Pairs {
t1 t2 e3, <Order t1 t2>:
{T = (t1 t2) <Pairs e3>;
F = (t2 t1) <Pairs e3>; };
t1 = (t1);
/* the odd term makes a separate list */
= ; }
Merge {
(e1)(e2)e.Rest =
(<Merge2 (e1)e2>) <Merge e.Rest>;
(e1) = (e1);
= ; }
* merge two lists
Merge2 {
(t1 eX) t2 eY, <Order t1 t2>:
{T = t1 <Merge2 (eX)t2 eY>;
F = t2 <Merge2 (t1 eX)eY>; };
(e1)e2 = e1 e2; /* One of e1,e2 is empty */
}
* Check whether there is one list or more
Check {
(e1) = e1;
e1 = <Check <Merge e1>>; }
Имеются и другие алгоритмы сортировки. Рассмотрим быструю сортировку. Выбирается первый терм в списке t1 и производится попытка разместить его на окончательное место. С этой целью оставшийся список делится на те термы, которые должны предшествовать t1 (назовем эту часть e.Left ), и на те, которые должны за ним следовать(назовем часть e.Right) . Тогда место t1 находится между этими двымя списками. Теперь остается применить эту процедуру рекурсивно к двум подспискам и произвести сцепление:
<Sort e.Left> t1 <Sort e.Right>
Ниже следует программа:
* Quick-sort
Sort {
= ;
t1 e2, <Partit ()t1()e2>: (eL)t1(eR)
= <Sort eL> t1 <Sort eR>;
* Partition list e.List by element sM.
* <Partit (e.Left)sM(e.Right)e.Remaining-list>
* == (e.Left1)sM(e.Right1)
Partit {
(eL)sM(eR) = (eL)sM(eR)
(eL)sM(eR) sX e2, <Order sX sM>:
{T = <Partit (eL sX)sM(eR) e2>;
F = <Partit (eL)sM(eR sX) e2>;
};
}
Для разбиения на части требуется время, пропорциональное длине списка. Суммарное время для разбиений на одном рекурсивном уровне приблизительно равно n. Так как e.Left и e.Right являются, в среднем, одинаковыми по длине, потребуется приблизительно log n уровней рекурсии. Отсюда полное время сортировки пропорционально n log n.
Ориентированный граф называется простым, если в нем существует не более чем одно ребро с данными начальной и конечной вершинами. Путь в таком графе определяется как последовательность вершин, в которой каждая следующая вершина достижима по ребру из предыдущей. Путь является ациклическим , если ни одна из его вершин не повторяется. Мы хотим определить функцию, которая для данного графа G и некоторой его вершины V будет перечислять все ациклические пути в G, начинающиеся с V.
Как всегда, первым, что следует выполнить, является представление объектов. Представим граф в формате
s.Vertex(e.List-of-next) ...
где e.List-of-next содержит все те вершины, которые могут быть достигнуты из s.Vertex по ребру (может быть, пустому). Например, граф на Рис. 5.1 представлен следующим образом:
A()B(A C)C(D E)D(C)E(A B D)

Рисунок 5.1 Ориентированный граф
Самым кратким решением проблемы является:
Paths {
eP(e1 sV e2)(e3 sV(e.Next)e4) =
<Paths eP sV (e.Next)(e3 e4)>
<Paths eP (e2)(e3 sV(e.Next)e4)>;
eP(e1)(e2) = (eP);
}
где начальный вызов должен иметь вид:
<Paths (V)(G)>
Для графа на Рис. 5.1 и начальной вершины E наша функция выдает результат:
(E A)(E B A)(E B C D)(E B C)(E B) (E D C)(E D)(E)()
Поясним, как мы приходим к следующему решению. Как это часто случается, прямое рекурсивное определение допустимо не только для сформулированной задачи, но и для ее обобщения. В нашем случае производится два обобщения: во-первых, вместо единственной начальной вершины V рассматривается список вершин Vlist, и требуется найти множество путей, которые могут начинаться с любой вершины, принадлежащей Vlist. Во-вторых, допускается произвольное начало P для вычисляемых путей. Таким образом, вызов
<Paths P(Vlist)(G)>
должен приводить к получению множества путей, каждый из которых начинается с P, затем проходит через некоторую вершину из Vlist и продолжается по графу G.
Идея алгоритма состоит в удалении из графа записей о тех вершинах, которые уже включены в какой-либо путь. При этом способе гарантируется, что в конструируемых путях не будет повторных вхождений вершин. В левой части предложения 1 находится образец, отыскивающий первую вершину sV , для которой еще возможно продолжение, так как имеется соответствующая запись в графе. Тогда искомое множество будет состоять из двух подмножеств, для которых записаны два параллельных рекурсивных вызова Paths : в первом sV добавляется к eP , e.Next становится множеством Vlist , и запись для sV исключается; во втором производится поиск других вершин во множестве Vlist без изменения графа G. Если возможных продолжений не осталось , выдается путь P.
Тем не менее, с точки зрения эффективности этот алгоритм имеет изъяны, поскольку для каждого рекурсивного шага процедуры Paths создается дополнительная копия графа (или того, что от него осталось). Этот недостаток исправлен в следующей программе:
$ENTRY Go { =
<Prout 'Type in the graph'>
<Br 'graph='<Input>>
<Prout 'Initial vertices, please'>
<Prout <Paths (<Input>)>>; }
$EXTRN Input;
Paths {
ePs1eQ(s1 e2) = <Paths ePs1eQ(e2)>;
eP(s1 e2) = <Paths ePs1 (<Next s1>)>
<Paths eP(e2)>;
eP() = (eP); }
Next {
sV, <Dg 'graph'>: e1 sV(eN) e2 = eN
<Br 'graph=' e1 sV(eN) e2>; }
Граф извлекается из аргумента Paths и
закапывается под именем'graph' . Каждый раз,
когда нужно построить продолжение для некоторой
вершины, применяется функция Next ,
которая копирует только подходящий фрагмент
описания графа. Поэтому на каждом рекурсивном
шаге процедуры Paths нужно проверить, что
вершина-кандидат не встречается в данном пути
(предложение 1).
Упражнение 5.2 Как вы могли бы уже заметить, в
обеих версиях Paths пустой путь является
элементом выходного множества. Хотя это
естественное следствие нашего рекурсивного
определения, оно может оказаться нежелательным.
Модифицировать программу (программы) таким
образом, чтобы исключить пустой путь.
5.4.ТРАНСЛЯЦИЯ АРИФМЕТИЧЕСКИХ ВЫРАЖЕНИЙ
Чтобы привести один из примеров программы-транслятора на РЕФАЛе, рассмотрим трансляцию арифметических выражений в язык ассемблера для одноадресного компьютера. Элементарными операндами в арифметических выражениях будут служить переменные (представленные идентификаторами) и целые числа. Допустимы пять арифметических операций: + , - , * , / , ^ (последний символ - для возведения в степень) с обычными правилами старшинства; могут также использоваться скобки.
Одноадресная вычислительная машина имеет накопитель и память. Компьютерный код состоит из операторов LOAD , STORE , ADD , SUB , MUL , DIV , POWER и MINUS , разделяемых точками с запятой. Оператор LOAD x , где x является адресом ячейки памяти, помещает значение, хранящееся в x, в накопитель; STORE x размещает содержимое накопителя в ячейке памяти с адресом x. Бинарные операторы выполняются над содержимым накопителя и некоторой ячейки памяти, а результат помещается в накопитель, например, SUB x вычитает содержимое x из накопителя и помещает разность обратно в накопитель. Оператор MINUS изменяет знак содержимого накопителя.
Мы будем транслировать арифметические выражения в язык ассемблера для описанной машины. Это значит, что вместо действительных машинных адресов будут использоваться символические адреса. Идентификаторы переменных будут использоваться в качестве их символических адресов. Вместо размещения констант по некоторому адресу и последующего использования этого адреса будут использоваться сами константы. Результат трансляции арифметического выражения представляет собой программу, которая вычисляет его значение и помещает его в накопитель. Например, выражение:
(x1 + 25)*factor
будет странслировано в:
LOAD x1; ADD 25; MUL factor;
Когда вычисляется арифметическое выражение, часто требуются дополнительные размещения в памяти для сохранения промежуточных результатов вычисления. Символическими адресами для таких размещений будут служить $1, $2, $3 ... и т.д. Результат трансляции выражения:
(a + 318)*(b - c)
будет выглядеть как:
LOAD b; SUB c; STORE $1; LOAD a; ADD 318; MUL $1;
Присвоим нашей программе-транслятору имя TRAREX . Далее приводится полный текст программы, сопровождаемый комментариями к ее составлению.
* Program TRAREX,
* Translation of arithmetic expressions
$ENTRY Go { = <Open 'r' 1 <Arg 1>>
<Open 'w' 2 <Arg 2>>
<Write <Translate <Input 1>>>; }
$EXTRN Input;
Translate {
= ;
e1 = <Code-gen (1) <Parse e1> <DG 'compl'>>
}
* Last symbol from a given list in expression
* <Last (e.Symb-List) e.Expr ()> == e1 sX(e2)
* where sX is the symbol looked for,
* and e1 sX e2 is e.Expr,
* or == (e.Expr)
* if there are no such at top level
Last {
(eA sX eB) e1 sX(e2) = e1 sX(e2);
(eA) e1 tX(e2) = <Last (eA) e1(tX e2)>;
(eA) (e2) = (e2); }
* <Parse e.Arithm-expr> == e.Tree
* e.Tree == s.Operation (e.Tree-1) e.Tree-2
* == s.Operand
* == empty
Parse {
e.Expr, <Last ('+-') e.Expr()>: e1 s.Op(e2) =
s.Op(<Parse e1>) <Parse e2>;
e.Expr, <Last ('*/') e.Expr()>: e1 s.Op(e2)
= s.Op(<Parse e1>) <Parse e2>;
e1'^'e2 = '^'(<Parse e1>) <Parse e2>;
s.Symb, <Type s.Symb>: 'F's.Symb = s.Symb;
s.Symb, <Type s.Symb>: 'N's.Symb = s.Symb;
(e.Expr) = <Parse e.Expr>;
= ;
e.Exp =
<Prout 'Syntax error.Cannot parse 'e.Exp>
<BR 'compl=' Fail>;
};
* Code generation.
* <Code-gen (sN) e.Parsing-tree>
* == assembler code
* sN is the number of the first location
* free for intermediate results.
Code-gen {
e1 Fail = ;
(sN) '-' ()e2 =
<Code-gen (sN) e2>
'MINUS ;';
(sN) s.Op(e1)s2 =
<Code-gen (sN) e1>
<Code-op s.Op> <Outform s2>';';
(sN) '+'(s1)e2 =
<Code-gen (sN) e2>
<Code-op '+'> <Outform s1>';';
(sN) '*'(s1)e2 =
<Code-gen (sN) e2>
<Code-op '*'> <Outform s1>';';
(sN) s.Op(e1)e2 =
<Code-gen (sN) e2>
'STORE $'<Symb sN>';'
<Code-gen (<Add (sN)1>) e1>
<Code-op s.Op> '$'<Symb sN>';';
(sN) s.Symb =
'LOAD '<Outform s.Symb> ';';
(sN) eX = (Synt-err)';';
};
* Convert operands into character strings
Outform {
sS, <Type sS>:
{'F'sS = <Explode sS>;
'N'sS = <Symb sS>; };
}
* Assembler codes of operations
Code-op {
'+' = 'ADD ';
'-' = 'SUB ';
'*' = 'MUL ';
'/' = 'DIV ';
'^' = 'POWER ';
};
* Write assembler code in a column
* (on screen and on disk)
Write {
(Synt-err)';' e2 = <Prout 'Syntax error'>;
e1';' e2 = <Prout <Put 2 e1>> <Write e2>;
= ; }
Эта программа читает выражение из одного файла и помещает результат трансляции в другой файл. Она также выводит результат трансляции на терминал. Программе требуется одна внешняя функция, Input , которая определена в модуле reflib , поставляемом с пакетом РЕФАЛ-системы; предполагается, что reflib.rsl размещен в текущей директории. Для того, чтобы вызвать trarex , следует ввести:
refgo trarex+reflib input-file output-file
Стартовая функция Go использует встроенную функцию Arg , чтобы сделать параметры, вводимые вместе с вызовом программы, доступными для РЕФАЛ-машины. <Arg 1> предназначен для входного файла, а <Arg 2> - для выходного файла. Функция Open назначает эти файлы для чтения и записи по каналам 1 и 2 соответственно.
Трансляция с одного языка программирования на другой включает следующие три этапа:
В нашем случае лексическими единицами являются
идентификаторы, целые числа, знаки операций и
круглые скобки. Функция Input полностью
осуществляет необходимый лексический анализ.
Она не только сворачивает строки символов,
представляющие идентификаторы и числа, в
неделимые символы-атомы, но и преобразует
символы-скобки в круглые РЕФАЛ-скобки, которые
надлежащим образом объединяются в пары. Такое
преобразование уже является началом
формирования синтаксического дерева; оно делает
более легким следующий этап синтаксического
анализа с помощью функции Parse.
ЗАМЕЧАНИЕ: Символ - на клавиатуре
используется и как дефис, и как знак минус. Первая
его функция используется в идентификаторах.
Поэтому x-1 будет восприниматься как
идентификатор. При использовании для вычитания
знак - окружается пробелами.
Входом для Parse служит результат функции Input . Ее выходом является синтаксическое дерево, которое должно использоваться функцией генерации кода Code-gen (см. определение функции Translate ). Следует выбрать точный формат этого дерева так, чтобы сделать генерацию кода более легкой.
Главным критерием для проектирования представления древовидного объекта в РЕФАЛе является то, что все варианты объекта, которые желательно различать в программах, должны быть различимы за счет применения простых образцов. Использование открытых e-переменных в образцах следовало бы ограничить, за исключением случаев, когда это совершенно необходимо; таких, например, как случай, когда ведется поиск элемента списка. Круглых скобок, не являющихся необходимыми, следует избегать. Часто в форматы объектов включается ряд символов для того, чтобы провести различие между вариантами и повысить читабельность. В нашем случае дерево имеет простую структуру. В процессе генерации кода нам нужно различать элементарные операнды и поддеревья. Используется формат, где элементарные операнды всегда являются символами, в то время как поддеревья никогда ими не являются. Таким образом, нет нужды в дополнительных средствах различения.
Случай элементарного операнда (листа дерева) задается следующей формулой:
e.Tree == s.Operand
а случай бинарной операции - формулой:
e.Tree == s.Operation (e.Tree-1) e.Tree-2
Следует также разрешить одну унарную операцию в арифметических выражениях: изменение знака, которое представлено тем же символом'-', что и бинарная операция вычитания. Когда проводится синтаксический анализ выражения, можно трактовать унарный минус таким же образом, что и бинарный; единственная разница между ними в том, что в случае унарного минуса первый опреанд является пустым. Поэтому добавляется еще один вариант для типа данных e.Tree :
e.Tree == - () e.Tree
и он рассматривается как отдельный случай на этапе генерации кода.
Проектируя структуры данных в РЕФАЛе, следует принимать в расчет как интересы функций, производящих эти структуры, так и интересы функций, их использующих. Часто случается, что структура, первоначально изобретенная в интересах одной из этих партий, требует модификаций для того, чтобы лучше удовлетворить потребности другой партии. Иногда вам придется произвести целый ряд таких подгонок перед тем как прийти к окончательным структурам данных, по мере того как вы вдаетесь в детали алгоритма. Это может потребовать некоторых усилий, но выигрышем для вас является лучшее представление и, почти наверняка, лучшее понимание алгоритма. Усилия эти окупятся во время тестирования и отладки.
При синтаксическом анализе используется способность РЕФАЛ-машины совершать скачок от левой или правой скобки к парной ей скобке и просматривать выражения как слева направо, так и справа налево. Для левоассоциативных операций, а именно, для + , - , * , и / , самая верхняя операция в дереве синтаксического разбора является последней на уровне главных скобок, например:
a - b - c = (a - b) - c
В этом выражении невозможно использовать открытые e-переменные для локализации нужного знака минус, потому что порядок слева-направо встроен в процедуру удлинения. Но можно производить просмотр терм за термом справа налево, пока не обнаружится первый минус. Это производится при помощи функции Last , которая обнаруживает последнее вхождение символа из данного перечня ("найти'' в РЕФАЛе означает поставить скобки в соответствующих местах). (Форма входа и выхода функции Last подробно описана в комментариях к программе.)
Операция возведения в степень ^ является правоассоциативной, поэтому при ее поиске в грамматическом разборе сверху-вниз можно использовать открытые переменные.
Все это ясно можно видеть в определении функции Parse . Каждое предложение в нем соответствует ситаксической категории исходного языка. Сперва выражение разделяется на части аддитивными операциями верхнего уровня + и - ; затем мультипликатиными операциями * и / . В третьем предложении уделено внимание операции ^ . Важен порядок этих предложений; он отражает отношение старшинства между операциями.
Но что делать с унарной операцией изменения знака? Она связывает сильнее, чем аддитивные или мультиприкативные операции, но слабее, чем операция возведения в степень. Одно из решений - добавить соответствующее предложение между вторым и третьим предложениями. Но тогда мы должны быть уверены, что первое предлождение не будет работать с пустым значением переменной e1 . Этого можно добиться, заменяя e1 на tX e1 . Однако мы применяем в программе другое решение. Просто разрешено первому (так же , как и второму) аргументу бинарных операций быть пустым, таким образом расширяется определение дерева грамматического разбора. Когда дело доходит до генерации кода, то разрешено только в одном случае листу дерева быть пустым - в случае унарного - .
Однако, такая простота не дается даром. Выражение типа ()-x будет считаться законным и эквивалентным -x . (О лучшем решении см. в упражнении далее.)
Остальные пять предложений Parse относятся к идентификаторам, числам, скобкам, пустым выражениям и ошибочным ситуациям.
Контроль ошибок является важной частью трансляции. В нашей программе лексические ошибки (включая непарные скобки) отлавливаются стандартной функцией Input . В процессе грамматического разбора в поле зрения может появиться много параллельных вызовов функции Parse . Если хотя бы при одном из таких вызовов встречается синтаксическая ошибка, не имеет смысла генерировать код. Программа должна выдать сообщение об ошибке и либо прекратитьпроцесс, либо продолжить грамматический разбор с целью обнаружения других возможных ошибок, но в любом случае прерывая генерацию кода. Вторая возможность предпочтительнее, и в нашей программе выбрана эта опция. Чтобы передать сообщение процедуре Code-gen , Parse закапывает символ Fail под именем 'compl' (сокращение от 'completion' - "завершение"). При вызове <Code-gen> 'compl' выкапывается и добавляется к правой части аргумента. Если ничего не было закопано (ошибок нет), добавление будет пустым. Первое предложение функции Code-gen проверяет, присутствует ли Fail, и если это так, заканчивает вычисление.
Функция Code-gen порождает ассемблерный код по дереву грамматического разбора арифметического выражения. Она имеет еще один аргумент - число, отмечающее первое свободное размещение для промежуточных результатов вычислений. Вначале оно равно 1 .
Когда наша учебная машина выполняет операцию, первый операнд находится в накопителе, а второй по определенному адресу. Однако хороший генератор кода должен был бы использовать коммутативность сложения и умножения и переставлять порядок операндов в случае, когда это может улучшить код. Например, при порядке операндов, заданном в выражении
a * (b - c)
результат трансляции имеет вид:
LOAD b; SUB c; STORE $1; LOAD a; MUL $1;
Вот, несомненно, лучший вариант трансляции:
LOAD b; SUB c; MUL a;
Это результат трансляции, который будет получен при выполнении нашей программы. В определении Code-gen имеются специальные предложения, отслеживающие ситуации, в которых инвертированный порядок более предпочтителен.
Некоторые ошибки не могут быть обнаружены
вплоть до этапа генерации кода, например, пустой
операнд (кроме случая пустого операнда для -
). Последнее предложение Code-gen обнаружит
такую ошибку, а функция вывода Write выдаст
на печать сообщение и остановится. Что касается
других предложений Code-gen , легче уяснить,
как они работают, из текста на РЕФАЛе , чем из
записываемых пояснений.
Упражнение 5.3 Модифицировать TRAREX
таким образом, чтобы она работала в
интерактивном режиме, запрашивая у пользователя
ввод выражения, транслируя его и снова
запрашивая, пока пользователь не наберет END
вместо выражения.
Упражнение 5.4 Как упомянуто выше, TRAREX
воспринимает ()-x как -x .
Модифицировать Parse так, чтобы пустое
подвыражение всегда рассматривалось как ошибка.